Các bài toán hình học liên quan đến chứng minh tứ giác nội tiếp đường tròn và tiếp tuyến của đường tròn luôn có khả năng xuất hiện trong đề thi môn Toán vào 10. Cùng thầy Nguyễn Quyết Thắng tổng hợp những kiến thức trọng tâm và giải các bài toán cụ thể được rút ra từ đề thi vào 10 những năm gần đây trong buổi livestream Bứt phá điểm thi vào 10 cùng HOCMAI môn Toán lúc 20h ngày thứ 4 (19/5).
Trong buổi livestream Bứt phá điểm thi vào 10 cùng HOCMAI môn Toán, thay vì tập trung vào những lý thuyết, định lý hình học, thầy Thắng đã tập trung vào những kiến thức trọng tâm liên quan đến các dạng bài thường gặp trong đề thi vào 10 môn Toán. Qua đó giúp các bạn học sinh rà soát kiến thức, hướng dẫn cách làm bài và tổng hợp những lưu ý quan trọng trong quá trình làm bài thi để các em tránh mất điểm đáng tiếc và chinh phục điểm tuyệt đối trong phần hình học.

Hệ thống kiến thức về 2 dạng bài thường gặp trong đề thi
Theo thầy Thắng, có 2 dạng bài hình học học sinh cần đặc biệt lưu ý vì nó thường xuyên xuất hiện trong đề thi của hầu hết các tỉnh thành là Tứ giác nội tiếp và tiếp tuyến đường tròn.
Tứ giác nội tiếp
Bên cạnh việc nắm vững các kiến thức nền tảng, kiến thức cơ bản, các tính chất trong sách giáo khoa, học sinh còn phải lưu ý đến phương pháp làm bài. Ví dụ, nếu đề bài yêu cầu chứng minh tứ giác nội tiếp thì các bạn phải định hình trong đầu là chúng ta có 3 hay 4 cách chứng minh. Tiếp đó, các bạn sẽ dựa vào những dữ liệu mà đề bài cho để tìm cách giải hợp lí nhất.
Các phương pháp chứng minh tứ giác nội tiếp:
- Chứng minh tứ giác nội tiếp có tổng hai góc đối bằng 180 độ.
Ví dụ: Có tứ giác ABCD và muốn chứng minh tứ giác đó nội tiếp đường tròn, học sinh phải chứng minh tổng góc A và góc C bằng 180 độ hoặc tổng góc B và góc D bằng 180 độ. Hoặc nếu 2 góc đối nhau có số đo góc là 90 độ thì lúc đó tứ giác ABCD sẽ nội tiếp đường tròn và đường kính sẽ là cạnh huyền của tam giác vuông.
- Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
Cách chứng minh thứ hai dựa trên nền tảng của cách một nhưng được phát triển theo một hướng nhìn khác để học sinh có nhiều hướng tư duy hơn khi làm một bài toán hình.
Ví dụ: Trong hình trên, khi kéo dài cạnh AD thì ở đỉnh D sẽ có 2 góc, góc D bên trong (góc trong) và một góc D bên ngoài kề bù với góc trong được gọi là góc ngoài đỉnh D.
Hai góc ở đỉnh D có tổng bằng 180 độ do đây là hai góc kề bù. Học sinh cần chứng minh góc ngoài đỉnh D bằng góc B, từ đó suy ra tổng góc B và góc D bên trong cũng bằng 180 độ. Và có thể kết luận tứ giác ABCD nội tiếp đường tròn.
- Chứng minh tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại những góc bằng nhau.
Ví dụ: Nối 2 đường chéo của tứ giác ABCD ta được đường chéo AC và đường chéo BD. Lúc này tam giác ABD có góc ABD “nhìn” cạnh AD, tam giác ACD có góc ACD cũng “nhìn” cạnh AD hoặc tư duy theo đường tròn thì góc ABD là góc nội tiếp chắn cung AD, góc ACD cũng là góc nội tiếp chắn cung AD. Và nếu góc ABD bằng góc ACD thì tứ giác ABCD sẽ là tứ giác nội tiếp.
- Chứng minh 4 đỉnh của tứ giác cách đều 1 điểm xác định.
Đây là cách “cổ điển” nhất bởi cách này dựa vào khái niệm, tính chất đường tròn để chứng minh. Tuy nhiên, đây là cách ít dùng nhất bởi trong đề bài hiếm khi tìm được 1 điểm nào đó và chứng minh được nó cách đều 4 đỉnh của tứ giác.
“Để chứng minh tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình: hình chữ nhật, hình vuông, hình thang cân” - một lưu ý nhỏ mà thầy Thắng gửi đến các bạn để phục vụ tốt hơn cho các bài toán chứng minh tứ giác nội tiếp.
Tiếp tuyến của đường tròn
- Chứng minh đường thẳng và đường tròn chỉ có một điểm chung (định nghĩa). Hoặc khoảng cách từ tâm đến đường thẳng đúng bằng bán kính: d = R.
- Chứng minh đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.
- Dựa vào tính chất góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn 1 cung.
Ví dụ: Cho đường thẳng xy cắt đường tròn tâm O tại điểm A, học sinh phải chứng minh được góc BAx bằng góc nội tiếp cùng chắn cung AB thì có thể suy ra Ax là tiếp tuyến của đường tròn tâm O.
Hướng dẫn phương pháp tư duy hình học qua ví dụ minh họa cụ thể
Trước khi bắt đầu hướng dẫn học sinh phương pháp làm bài, thầy Thắng cũng chia sẻ về quan điểm của mình về việc giảng dạy.
“Thầy không mong muốn học sinh học mình sẽ hỏi “đáp án là gì?” mà sẽ phải tự đặt câu hỏi vì sao có được lời giải đó. Việc đưa ra đề bài và chiếu đáp án không khác gì đưa cho các em đọc 1 cuốn sách giải. Thay vì đó, thầy sẽ là người cùng các em tìm ra con đường và lý giải cho các em tại sao lại có đáp án đó. Thầy sẽ cố gắng giảng dạy sao cho các em hiểu rõ vấn đề một cách đơn giản nhất, tiếp thu kiến thức một cách nhẹ nhàng nhất.”
Với tinh thần này, thầy Thắng đã đồng hành cùng các em đi từng bước, từ khảo sát đề bài, hướng dẫn vẽ hình, đưa ra phương pháp tư duy và hướng dẫn trình bày với ví dụ sau:
Ví dụ: Cho (O;R) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O;R) sao cho đoạn thẳng AC cắt đường tròn (O;R) tại điểm K (K khác A), hai dây MN và BK cắt nhau tại E.
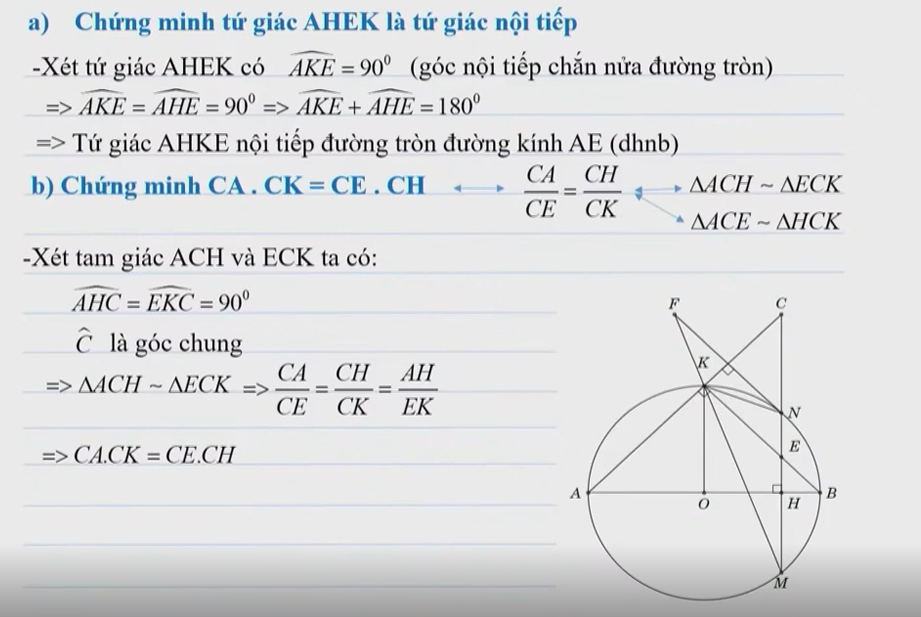
a) Chứng minh tứ giác AHEK là tứ giác nội tiếp
b) Chứng minh CA.CK=CE.CH
c) Qua điểm N kẻ đường thẳng d vuông góc với AC, d cắt tia MK tại F. Chứng minh tam giác NFK cân
d) Khi KE=KC, chứng minh rằng OK//MN
Lời giải
a) Chứng minh tứ giác AHEK là tứ giác nội tiếp
Đây là kiến thức trọng tâm và cũng là dạng toán điển hình trong đề thi vào 10 của nhiều tỉnh thành.
Với bài này, học sinh cần rà soát lại những phương pháp chứng minh tứ giác nội tiếp đã được thầy Thắng đề cập đến ở phần trước đó, bám sát vào cơ sở lý thuyết và đặc biệt là phương pháp chứng minh để tìm ra lời giải.
b) Chứng minh CA.CK = CE.CH
Học sinh nắm chắc kiến thức phần hình học từ lớp 8 sẽ biết cách làm câu này. Khi đề bài yêu cầu chứng minh tích của 2 đoạn thẳng bằng nhau, chúng ta có 3 hướng làm:
- Dùng hệ thức lượng: Chỉ áp dụng trong trường hợp là tam giác vuông, có đường cao
- Áp dụng định lý Talet
- Chứng minh tam giác đồng dạng: Đây chính là chìa khóa và phương pháp thường xuyên được sử dụng để xử lý những dạng bài thế này.
Đặc biệt với câu hỏi này, thầy Thắng đã hướng dẫn học sinh sử dụng phương pháp tư duy ngược. Đây cũng chính là 1 trong những điểm nổi bật và đặc sắc trong phong cách giảng dạy của thầy, khi đưa ra các ví dụ, sau đó phân tích, so sánh từ đó đưa ra các kết luận giúp học sinh kiểu kiến thức. Từ những phân tích, so sánh thầy sẽ tổng hợp lại kiến thức giúp học sinh hiểu sâu, nắm chắc kiến thức trong từng bài học.
c) Chứng minh tam giác NFK cân
Để chứng minh tam giác cân, chúng ta có 3 cách:
- Chứng minh 2 cạnh bằng nhau
- Chứng minh 2 góc bằng nhau
- Chứng minh tam tam giác có 1 đường cao đồng thời là trung tuyến/ phân giác/ trung trực.
Với bài Toán này, thầy Thắng lựa chọn phương pháp chứng minh 2 góc bằng nhau. Cụ thể như sau:

d) Khi KE=KC, chứng minh rằng OK//MN
Hướng tư duy để làm bài này là học sinh phải bám vào điều kiện đã cho ở đề bài để suy ra kết luận:
Khi KE = KC => tam giác CKE vuông cân tại K
=> KCE = KEC = 45० => KAB = KBA = 45०
=> Tam giác KAB vuông cân tại K
=> KO là trung tuyến đồng thời là đường cao của tam giác AKB
=> KO vuông góc AB mà CM vuông góc AB => KO // CM
Phụ huynh, học sinh xem hướng dẫn giải chi tiết ví dụ trên trong video dưới đây:
Lưu ý để làm tốt phần Hình học trong đề thi vào lớp 10
Trong cấu trúc đề thi vào 10 môn Toán, phần Hình học thường sẽ có 4 câu và chiếm 3,5 điểm, tương tự như ví dụ thầy Thắng đã phân tích. Trong đó 1 điểm thường là nhận biết - thông hiểu, 2 điểm thuộc mức độ vận dụng còn 0,5 điểm ở mức vận dụng cao.
Ngoài ra, một số tỉnh đang có xu hướng thi hình không gian thì sẽ bớt 0,5 điểm ở phần vận dụng cao, thay vào đó là câu hỏi về hình không gian, ví dụ như Hà Nội, TP.HCM cũng thi vào hình không gian. Vì vậy học sinh ở các tỉnh/thành phố khác cần lưu ý điều này.
Nếu như phần Đại số đòi hỏi học sinh phải thuộc lòng các công thức thì các bài toán hình học thi vào 10 lại yêu cầu cao hơn hẳn. Không những phải nắm được các định lí mà còn phải biết vận dụng linh hoạt vào các dạng bài chứng minh hình học. Điều quan trọng nhất để làm tốt phần hình học, bên cạnh việc nắm chắc kiến thức lý thuyết, thuộc và hiểu các định lý là học sinh cần tìm ra hướng tư duy để xử lý bài toán hình, nắm chắc các phương pháp chứng minh để có cơ sở rà soát và lựa chọn phương pháp tối ưu nhất cho từng bài.
Hy vọng với những chia sẻ và hướng dẫn của thầy Thắng về phương pháp giải quyết bài toán Hình học trong đề thi vào lớp 10, các bạn học sinh sẽ không còn cảm thấy “e ngại” với câu hỏi hình học và tự tin hơn để bứt phá điểm số trong bài thi vào 10 môn Toán.


