Tam giác vuông là một tam giác có một góc là góc vuông (góc 90 độ). Mối quan hệ giữa các cạnh và góc của một tam giác vuông là nền tảng cơ bản của lượng giác học.
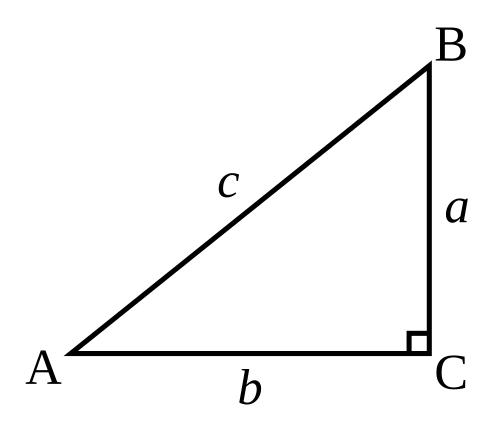
Cạnh đối diện với góc vuông gọi là cạnh huyền. Hai cạnh kề với góc vuông là cạnh bên (hay còn gọi là cạnh góc vuông). Cạnh a có thể xem là kề với góc B và đối góc A, trong khi cạnh b kề góc A và đối góc B.
Nếu chiều dài của ba cạnh là các số nguyên, tam giác được gọi là tam giác Pythagoras và chiều dài ba cạnh của nó được gọi chung là Bộ ba số Pythagoras.
Trong tam giác vuông, 2 góc nhọn phụ nhau (có tổng số đo bằng 90 độ).
Nếu một đường cao được vẽ từ đỉnh góc vuông cho tới cạnh huyền thì tam giác vuông được chia thành hai tam giác nhỏ hơn đồng dạng với tam giác gốc và đồng dạng với nhau. Từ đó:
- Chiều cao là trung bình nhân của hai đoạn cạnh huyền.
- Mỗi cạnh của tam giác vuông là trung bình nhân của cạnh huyền và hai đoạn của cạnh huyền kề với cạnh bên.
Công thức được viết là:
f 2 = d e , {displaystyle displaystyle f^{2}=de,} (Đôi khi được gọi là Định lý đường cao tam giác vuông) b 2 = c e , {displaystyle displaystyle b^{2}=ce,} a 2 = c d {displaystyle displaystyle a^{2}=cd}
a 2 = c d {displaystyle displaystyle a^{2}=cd} 
Trong đó, a, b, c, d, e, f được thể hiện như trong biểu đồ. Do đó:
f c = a b . {displaystyle fc=ab.}Hơn nữa, chiều cao với cạnh huyền còn có liên quan tới các cạnh bên của tam giác vuông, cụ thể:[1][2]
1 a 2 + 1 b 2 = 1 f 2 . {displaystyle {frac {1}{a^{2}}}+{frac {1}{b^{2}}}={frac {1}{f^{2}}}.}Với bất cứ tam giác nào, diện tích đều bằng một nửa chiều dài đáy nhân với chiều cao tương ứng. Trong một tam giác vuông, nếu một cạnh góc vuông được coi là đáy thì cạnh góc vuông còn lại được xem là chiều cao, diện tích của tam giác vuông khi đó sẽ bằng một nửa tích của hai cạnh góc vuông. Công thức diện tích của tam giác là:
S = a b 2 = c h 2 {displaystyle S={frac {ab}{2}}={frac {ch}{2}}}
Trong đó a và b là 2 cạnh góc vuông của tam giác, c là cạnh huyền và h là đường cao của tam giác
Nếu đường tròn nội tiếp tiếp tuyến cạnh huyền AB tại điểm P, coi nửa chu vi là s = (a+b+c)/2, chúng ta có PA = s − a và PB = s − b và diện tích sẽ là:
S = PA ⋅ PB = ( s − a ) ( s − b ) . {displaystyle S={text{PA}}cdot {text{PB}}=(s-a)(s-b).}
Công thức này chỉ áp dụng với các tam giác vuông.[3]
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Định lý Pythago phát biểu rằng:
Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này. (xem hình 3)Nó được thể hiện bằng phương trình a 2 + b 2 = c 2 {displaystyle displaystyle a^{2}+b^{2}=c^{2}} trong đó, c là chiều dài của cạnh huyền và a và b là chiều dài của hai cạnh còn lại.
Bán kính của đường tròn nội tiếp của một tam giác vuông với hai cạnh bên a và b và cạnh huyền c là:
r = a + b − c 2 = a b a + b + c . {displaystyle r={frac {a+b-c}{2}}={frac {ab}{a+b+c}}.}Bán kính của đường tròn ngoại tiếp bằng chiều dài một nửa cạnh huyền
R = c 2 . {displaystyle R={frac {c}{2}}.}Trong tam giác vuông có góc nhọn α {displaystyle alpha } thì
sin α {displaystyle sin alpha } = cạnh đối/cạnh huyền
cos α {displaystyle cos alpha } = cạnh kề/cạnh huyền
tan α {displaystyle tan alpha } = cạnh đối/cạnh kề
cot α {displaystyle cot alpha } = cạnh kề/cạnh đối .
Có một bài thơ giúp ta nhớ được: "Sin đi học / Cos không hư / Tan đoàn kết / Cot kết đoàn''.
- Tam giác có 1 góc vuông là tam giác vuông.
- Tam giác có 2 góc nhọn phụ nhau là tam giác vuông.
- Tam giác có bình phương độ dài 1 cạnh bằng tổng bình phương độ dài 2 cạnh kia là tam giác vuông (định lý Pythagoras đảo).
- Tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy là tam giác vuông.
- Tam giác nội tiếp đường tròn có 1 cạnh là đường kính thì tam giác đó vuông.
- Tam giác có cạnh đối diện góc 30° bằng một nửa một cạnh khác trong tam giác thì tam giác đó vuông.
- Tam giác là tam giác vuông khi và chỉ khi chúng có một góc bằng tổng hai góc còn lại.
- Calculator for right triangles Lưu trữ ngày 30 tháng 9 năm 2017 tại Wayback Machine


