1. Ba trường hợp bằng nhau của tam giác vuông
Hoạt động 1 trang 75 Toán 7 Tập 1
2. Trường hợp bằng nhau đặc biệt của tam giác vuông
Hoạt động 4 trang 78 Toán 7 Tập 1
Vẽ tam giác vuông ABC có A = 90°, AB = 3 cm, BC = 5 cm theo các bước sau:
• Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm.
• Vẽ tia Ax vuông góc với AB và cung tròn tâm B bán kính 5 cm như Hình 4.51.
Cung tròn cắt tia Ax tại điểm C.
•Vẽ đoạn thẳng BC ta được tam giác ABC.
Hướng dẫn giải:
Hoạt động 5 trang 78 Toán 7 Tập 1
Giải bài tập trang 79 Toán 7 tập 1 KNTT
Bài 4.20 trang 79 Toán 7 tập 1 KNTT
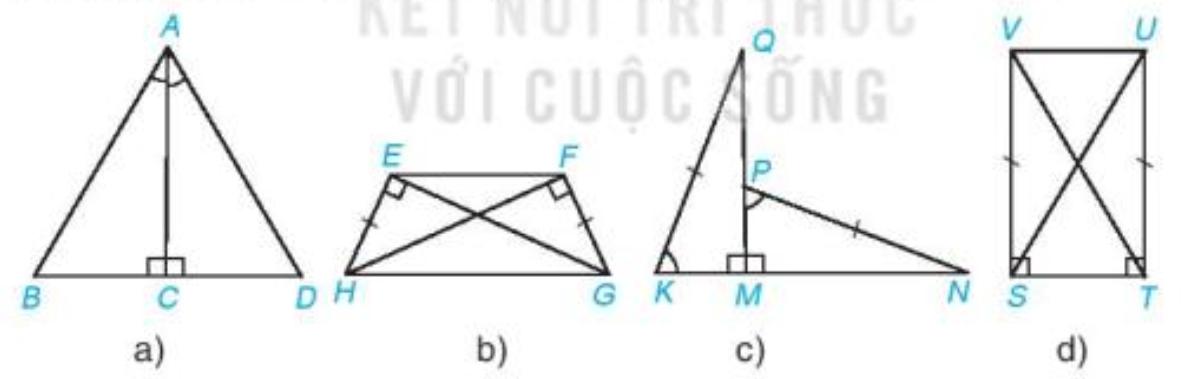
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
Hướng dẫn giải:
a) Xét 2 tam giác vuông ABC và ADC có:
AC chung
(widehat {BAC} = widehat {DAC}(gt))
b) Xét 2 tam giác vuông HEG và GFH có:
HE=GF(gt)
HG chung
(=>Delta HEG = Delta GFH(c.h-c.g.v))
c) Xét 2 tam giác vuông QMK và NMP có:
QK=NP
(widehat K = widehat P)
(=>Delta QMK = Delta NMP)(cạnh huyền - góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
VS=UT
ST chung
(=>Delta VST = Delta UTS(c.g.c))
Bài 4.21 trang 79 Toán 7 tập 1 KNTT
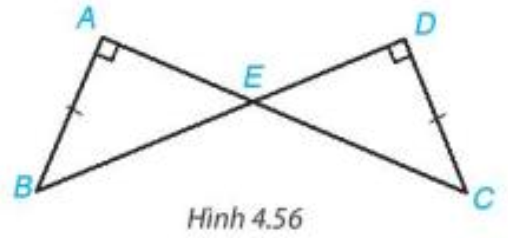
Cho hình 4.56, biết (AB=CD, widehat {BAC} = widehat {BDC} = {90^o}). Chứng minh rằng (Delta ABE = Delta DCE).
Hướng dẫn giải:
Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AED và DEC có:
(widehat {AEB} = widehat {DEC})(đối đỉnh) và (widehat {BAC} = widehat {BDC} = {90^o}).
Suy ra: (widehat {AEB} = widehat {DEC})
Xét 2 tam giác vuông AEB và DEC có:
AB=DC
(widehat {AEB} = widehat {DEC})
(=>Delta AEB = Delta DEC(g.c.g))
Bài 4.22 trang 79 Toán 7 tập 1 KNTT
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Chứng minh rằng (Delta ABM = Delta DCM).
Hướng dẫn giải:
Xét 2 tam giác vuông ABM và DCM có:
AB=DC (tính chất hình chữ nhật)
BM=CM (gt)
(=>Delta ABM = Delta DCM(c.g.c))
