Chuyên đề nhân liên hợp cơ bản phương trình

Sử dụng biểu thức nhân liên hợp để giải toán chứa căn bậc hai, căn bậc ba
Với Sử dụng biểu thức nhân liên hợp để giải toán chứa căn bậc hai, căn bậc ba môn Toán lớp 9 sẽ giúp học sinh nắm vững lý thuyết, biết phương pháp làm các dạng bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 9.
I. Lý thuyết
Một số biểu thức liên hợp thường gặp:

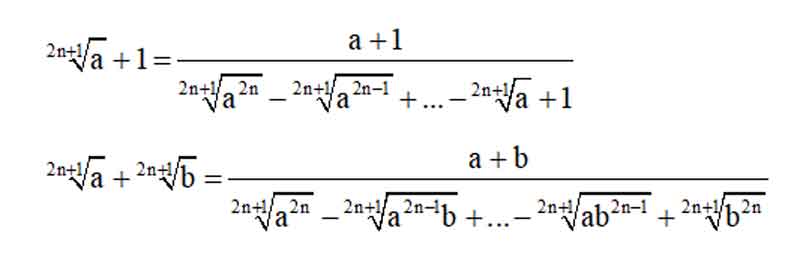
II. Dạng bài tập
Dạng 1: Sử dụng căn bậc 2, căn bậc 3 để tính giá trị biểu thức.
Phương pháp giải: Sử dụng các phép nhân liên hợp để biến đổi biểu thức ban đầu thành những biểu thức đơn giản hơn sau đó thực hiện theo thứ tự phép tính.
Ví dụ: Tính



Dạng 2: Sử dụng biểu thức nhân liên hợp để rút gọn biểu thức có chứa căn bậc 2, căn bậc 3.
Phương pháp giải: Dùng biểu thức liên hợp để biến đổi và rút gọn biểu thức.
Ví dụ: Rút gọn biểu thức sau:



Dạng 3: Chứng minh x0 là nghiệm của phương trình
Phương pháp giải: Dùng các biểu thức liên hợp để đưa nghiệm x0 về số đơn giản có thể tính toán được. Sau đó thay x0 vào phương trình và chứng minh x0 là nghiệm.


GIA SƯ TOÁN LỚP 9
Giải phương trình bằng phương pháp nhân liên hợp
Nhân liên hợp để giải phương trình, bất phương trình chứa căn là một trong những phương pháp hiệu quả để giải phương trình, khi mà chúng ta nhận thấy ngay được một nghiệm đẹp của phương trình, bất phương trình đã cho.
1. Các bước giải phương trình, bất phương trình bằng nhân liên hợp
Ý tưởng của phương pháp nhân liên hợp là khi một phương trình, bất phương trình chứa căn thức mà có nghiệm đẹp thì thường ta sẽ tìm cách phân tích thành nhân tử. Nhưng đối với một đa thức thì việc phân tích đa thức thành nhân tử sẽ dễ dàng hơn so với các biểu thức chứa căn, do đó chúng ta sẽ tìm cách khử căn thức bằng cách nhân chia với biểu thức liên hợp.

- Bước 1. Nhẩm nghiệm hoặc dùng máy tính để tìm nghiệm của phương trình, giả sử nghiệm của pt là x0.
- Bước 2. Phân tích (tách hoặc thêm bớt các hạng tử thích hợp), sau đó nhân chia với biểu thức liên hợp sao cho sau khi nhân chia liên hợp ta được có biểu thức có chứa nhân tử x-x0.
2. Ví dụ giải phương trình nhân liên hợp
Ví dụ 1. Giải phương trình
Hướng dẫn. Chúng ta đoán (hoặc dùng lệnh SOLVE của máy tính CASIO) và nhận thấy phương trình có nghiệm x=2. Tức là, chắc chắn phương trình sẽ có nhân tử là (x−2), nhưng chúng ta khó phân tích biểu thức chứa căn thành nhân tử, nên sẽ tìm cách chuyển về đa thức rồi phân tích. Cụ thể, chúng ta tách 11=8+3 rồi biến đổi như sau
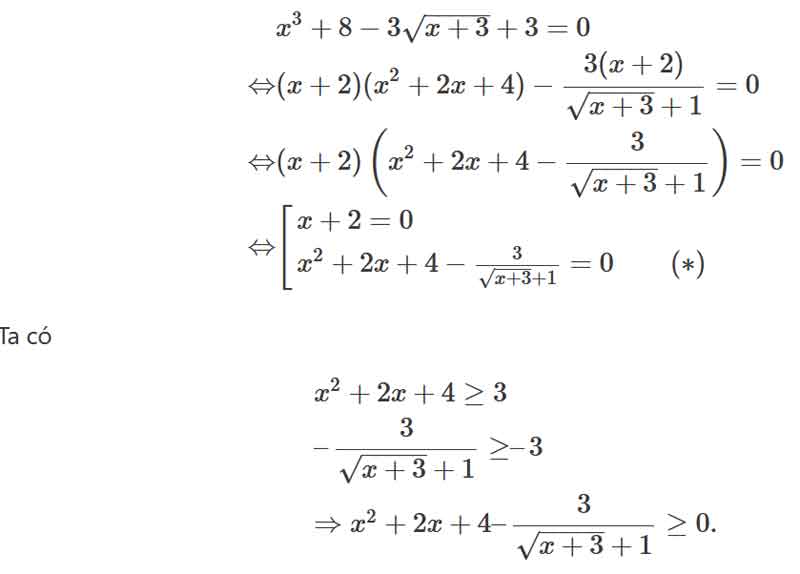
Bất phương trình cuối không xảy ra dấu đẳng thức nên phương trình (*) vô nghiệm.
Vậy phương trình đã cho có nghiệm duy nhất x=2.
Ví dụ 2. Giải phương trình





do đó phương trình đã cho có nghiệm duy nhất x=5.
Đôi khi, sau khi nhân chia liên hợp, việc chứng minh phương trình còn lại vô nghiệm khá khó khăn, ta hãy xem ví dụ sau.
Ví dụ 7. Giải phương trình




Hướng dẫn. Điều kiện x≥1, nhân liên hợp cho vế trái thì bất phương trình đã cho tương đương với


3. Bài tập phương pháp nhân liên hợp giải phương trình, bất phương trình
Đối với các bải tập sau, ta có thể sử dụng phương pháp nhân chia với biểu thức liên hợp để giải quyết.




Công thức toán
Gia sư môn toán
Công thức biến đổi tích thành tổng
Công thức nhân liên hợp
CÔNG THỨC LƯỢNG GIÁC


