
Lý thuyết Nhị thức Newton – Toán 10 Chân trời sáng tạo
Lý thuyết Toán 10 Bài 3: Nhị thức Newton - Chân trời sáng tạo
A. Lý thuyết Nhị thức Newton
1. Định nghĩa Nhị thức Newton
Nhị thức Newton là một định lý toán học quan trọng liên quan đến khai triển hàm mũ của tổng và phân tích các đa thức bậc cao. Định lý Nhị thức Newton có ứng dụng rộng rãi trong toán học và nhiều lĩnh vực khác, bao gồm:
+ Tính tổ hợp và chỉnh hợp: Định lý Nhị thức Newton là công cụ quan trọng trong việc tính toán số cách sắp xếp hoặc chọn k phần tử từ n phần tử mà không quan trọng thứ tự, điều này có ứng dụng trong nhiều vấn đề tổ hợp và chỉnh hợp.
+ Dãy số: Định lý Nhị thức Newton thường được sử dụng để chứng minh các thuộc tính của các dãy số, ví dụ như dãy số Fibonacci và dãy số Pascal.
+ Xác suất và thống kê: Trong xác suất và thống kê, định lý Nhị thức Newton được sử dụng để tính xác suất và biểu diễn các phân phối xác suất, nhất là trong việc tính toán xác suất của các biến ngẫu nhiên rời rạc.
+ Lý thuyết đồ thị: Công thức Nhị thức được sử dụng để tính toán số lượng đồ thị con trong một đồ thị, điều này có ứng dụng trong lý thuyết đồ thị và các vấn đề liên quan đến mạng lưới.
2. Công thức Nhị thức Newton
Với a,b là những số thực tùy ý và với mọi số tự nhiên n≥1, ta có:
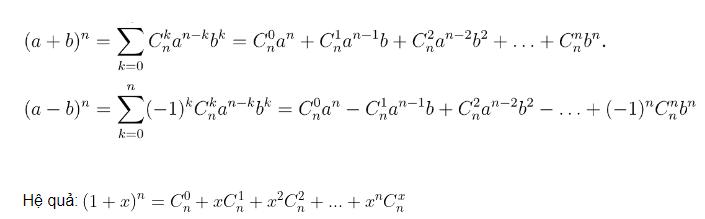
Hai công thức khai triển:
• a+b4=C40a4+C41a3b+C42a2b2+C43ab3+C44b4
=a4+4a3b+6a2b2+4ab3+b4;
• a+b5=C50a5+C51a4b+C52a3b2+C53a2b3+C54ab4+C55b5
=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) a+bn ứng với n = 4 và n = 5.
Chú ý:
- Các hệ số trong khai triển nhị thức Newton (a + b)n với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).
Bảng số trên dược gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 - 1662).
Ví dụ: Sử dụng công thức nhị thức Newton khai triển biểu thức (a + 2)4.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
(a + 2)4 = 1.a4 + 4a3.2 + 6a2.22 + 4a.23 + 24
= a4 + 8a3 + 24a2 + 32a + 16.
Ví dụ: Khai triển và rút gọn biểu thức: 1+55+1−55.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
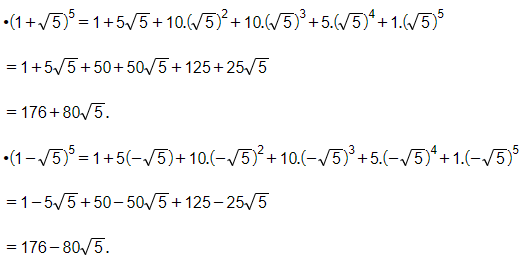
Do đó ta có: 1+55+1−55=176+805+176−805=352.
B. Các dạng bài toán Nhị thức Newton
1. Bài toán tìm số hạng thứ k trong khai triển nhị thức Newton
Bước 1: Khai triển nhị thức newton để tìm số hạng tổng quát: Khai triển nhị thức newton
Bước 2: Dựa vào đề bài, giải phương trình hai số mũ bằng nhau Số hạng chứa xm ứng với giá trị k thỏa: np - pk + qk = m. Từ đó tìm k=m−npq−p
Vậy số hạng chứa xm là: với giá trị k đã tìm được ở trên. Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm, hệ số phải tìm bằng 0
Chú ý: Xác định hệ số của số hạng chứa xm trong khai triển P(x) = (a + bxp + cxq)n được viết dưới dạng a0 + a1x + …+ a2nx2n
Ta làm như sau:
Viết
Viết số hạng tổng quát khi khai triển các số hạng dạng bxp + cxq Thành một đa thức theo lũy thừa của x Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm
Chú ý: Để xác định hệ số lớn nhất trong khai triển nhị thức newton
Ta làm như sau: Tính hệ số ak theo k và n. Giải bất phương trình sau với ẩn số k.ak-1≤ak
Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thỏa mãn bất phương trình trên.
2. Bài toán tìm hệ số trong khai triển nhị thức Newton
Tìm hệ số xk trong khai triển nhị thức newton
Phương pháp chung: Sử dụng công thức khai triển nhị thức newton. Tìm số hạng có chứa xk và tìm hệ số tương ứng.
Ví dụ: Tìm hệ số của x3 trong khai triển (2 + x)5
Giải: Ta có
Cho k = 3 ta được hệ số của x3 là: C35. 25-3 = 40
3. Bài toán tính tổng, chứng minh đẳng thức
Phương pháp giải:
Sử dụng khai triển:
(a + b)n = C0n an + C1n an-1b + C2n an-2b2 + …+ Cn-1 n abn-1 + Cnn bn
Suy ra điều phải chứng minh. Bằng cách thay a, b, n bằng các giá trị thích hợp ta sẽ được các đẳng thức. Bài toán ứng dụng nhị thức newton trong các bài liên quan đến tổ hợp
4. Bài toán ứng dụng nhị thức newton trong các bài liên quan đến tổ hợp
Cho một khai triển (a + x)n phù hợp, ở đây a là hằng số. Sử dụng các phép biến đổi đại số hoặc lấy đạo hàm, tích phân. Dựa vào điều kiện bài toán, thay x bởi một giá trị cụ thể
C. Bài tập tự luyện
Bài 1. Sử dụng công thức nhị thức Newton khai triển biểu thức:
a) (2x + y)4;
b) x−55.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
a) (2x + y)4 = (2x)4 + 4.(2x)3.y + 6.(2x)2.y2 + 4(2x).y3 + y4
= 16x4 + 32x3y + 24x2y2 + 8xy3 + y4.
Bài 2. Tìm hệ số của x4 trong khai triển (2x - 3)5.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
(2x - 3)5 = (2x)5 + 5(2x)4.(-3) + 10.(2x)3.(-3)2 + 10.(2x)2.(-3)3 + 5.2x.(-3)4 + (-3)5
= 32x5 - 240x4 + 720x3 - 1080x2 + 810x - 243
Vậy hệ số của x4 trong khai triển là -240.
Bài 3. Sử dụng công thức nhị thức Newton chứng tỏ rằng:
C50+2.C51+22.C52+23.C53+24.C54+25.C55=243
Hướng dẫn giải
Giả sử ta có khai triển (a + b)n với n = 0; 1; 2; …
Ta thấy trong biểu thức chứng minh có tổ hợp chập k của 5, nên n = 5.
Ở đây có xuất hiện lũy thừa của số 2 từ mũ 1 đến mũ 5 nên b = 2.
Ta có khai triển:
a+25=C50.a5+C51.a4.2+C52.a3.22+C53.a2.23+C54.a.24+C55.25
Khi a = 1 thì ta có:
1+25=C50.15+C51.14.2+C52.13.22+C53.12.23+C54.1.24+C55.25
⇔35=C50+2.C51+22.C52+23.C53+24.C54+25.C55
⇔243=C50+2.C51+22.C52+23.C53+24.C54+25.C55
Vậy C50+2.C51+22.C52+23.C53+24.C54+25.C55=243.
Bài 4. Khai triển và rút gọn biểu thức: (x + 2)4 + (2 - x)4.
Từ đó tính giá trị biểu thức: 2,054 + 1,954.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
• (x + 2)4 = x4 + 4x3.2 + 6x2.22 + 4x.23 + 24
= x4 + 8x3 + 24x2 + 32x + 16.
• (2 - x)4 = 24 + 4.23.(-x) + 6.22.(-x)2 + 4.2.(-x)3 + (-x)4
= x4 - 8x3 + 24x2 - 32x + 16.
Do đó ta có:
(x + 2)4 + (2 - x)4 = 2x4 + 48x2 + 32.
Với x = 0,05 ta có:
(0,05 + 2)4 + (2 - 0,05)4
= 2.(0,05)4 + 48.(0,05)2 + 32
= 32,1200125.
Vậy 2,054 + 1,954 = 32,1200125.
Xem thêm tóm tắt lý thuyết Toán lớp 10 sách Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài tập cuối chương 8
Lý thuyết Bài 1: Tọa độ của vectơ
Lý thuyết Bài 2: Đường thẳng trong mặt phẳng tọa độ
Lý thuyết Bài 3: Đường tròn trong mặt phẳng tọa độ
Lý thuyết Bài 4: Ba đường conic trong mặt phẳng tọa độ
Link nội dung: https://studyenglish.edu.vn/index.php/toan-10-nhi-thuc-newton-a46068.html