
Nằm lòng mọi cách giải phương trình mũ và logarit
Đầu tiên, các em cùng VUIHOC đọc bảng dưới đây để có nhận định tổng quan về lý thuyết và các bài tập áp dụng giải phương trình mũ và logarit nhé!
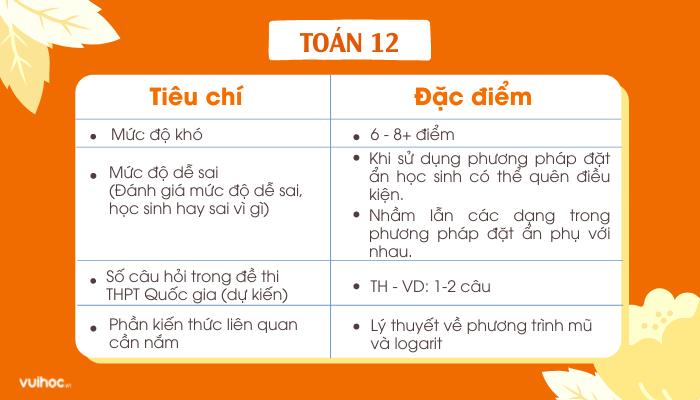
Để tiện hơn cho ôn tập, các em tải file tổng hợp lý thuyết chung về phương trình mũ logarit và cách giải phương trình mũ và logarit dưới đây nhé!
Tải xuống file tổng hợp lý thuyết phương trình mũ và logarit
1. Ôn tập lý thuyết chung về phương trình mũ và logarit
1.1. Lý thuyết phương trình mũ
Về định nghĩa:
Hiểu đơn giản, phương trình mũ là dạng phương trình 2 vế trong đó có chứa biểu thức mũ.
Theo định nghĩa đã được học trong chương trình THPT, ta có định nghĩa và dạng tổng quát chung của phương trình mũ như sau:
Phương trình mũ có dạng $a^x=b$ với $a,b$ cho trước và $0<aneq 1$
Phương trình mũ có nghiệm khi:
-
Với $b>0$: $a^x=bRightarrow x=log_ab$
-
Với $bleq 0$: phương trình mũ vô nghiệm
Các công thức phương trình mũ cơ bản cần nhớ:
Để giải phương trình mũ, các em cần ghi nhớ các công thức cơ bản của số mũ phục vụ áp dụng trong các bước biến đổi. Công thức mũ cơ bản được tổng hợp trong bảng sau:

Ngoài ra, các tính chất của số mũ cũng là một phần kiến thức cần nhớ để giải phương trình mũ. Tổng hợp tính chất của số mũ được VUIHOC liệt kê theo bảng dưới đây:
Các em cần lưu ý, các tính chất trên áp dụng khi số mũ đó đã xác định nhé!
1.2. Lý thuyết phương trình logarit giải phương trình mũ logarit
Về định nghĩa:
Với cơ số a dương và khác 1 thì phương trình có dạng như sau được gọi là phương trình logarit cơ bản $log_ax=b$
Ta thấy vế trái của phương trình là hàm đơn điệu có miền giá trị là mathbb{R}. Vế phải phương trình là một hàm hằng. Vì vậy phương trình logarit cơ bản luôn có nghiệm duy nhất. Theo định nghĩa của logarit ta dễ dàng suy ra nghiệm đó là $x=a^b$
Với điều kiện 0<a ≠ 1, ta có các phương trình logarit cơ bản như sau:
Hai quy tắc tính logarit quan trọng dùng để biến đổi phương trình logarit mà các em cần ghi nhớ:
- Quy tắc logarit của 1 tích:
- Công thức logarit của một tích như sau: $log(ab)=log(a)+log(b)$.
- Điều kiện: $a, b$ đều là số dương
- Đây là logarit hai số a và b thực hiện theo phép nhân thông qua phép cộng logarit ra đời vào thế kỷ 17. Sử dụng bảng logarit, ta sẽ đưa logarit về cơ số $a=10$ là logarit thập phân sẽ dễ dàng tra bảng, tính toán hơn. Logarit tự nhiên với hằng số $e$ là cơ số (khoảng bằng 2,718) được áp dụng thuận tiện trong toán học. Logarit nhị phân có cơ số 2 được dùng trong khoa học máy tính.
- Nếu muốn thu nhỏ phạm vi các đại lượng, bạn dùng thang logarit.
- Quy tắc logarit của 1 luỹ thừa:
- Ta có công thức logarit như sau: $log_{alpha}ab=log_{alpha}a+log_{alpha}b$
- Điều kiện với mọi số α và $0<aneq 1,b>0$ .
Đối với phương trình logarit giải phương trình mũ logarit, chúng ta cần lưu ý thêm các công thức dưới đây:
2. Các dạng bài tập giải phương trình mũ và logarit
2.1. Phương pháp giải phương trình mũ
Dạng 1: Dạng toán đưa về cùng cơ số
Ở phương pháp giải phương trình mũ này, ta cần biến đổi theo công thức sau để đưa về cùng cơ số:
Với $a>0$ và a ≠ 1 ta có $a^{f(x)}=a^{g(x)}Rightarrow f(x)=g(x)$
Ta cùng xét ví dụ sau đây để hiểu rõ cách giải phương trình mũ đưa về cùng cơ số này:
Dạng 2: Dạng toán đặt ẩn phụ giải phương trình mũ logarit
Đây là phương pháp giải phương trình mũ và logarit thường gặp trong các đề thi. Chúng ta thường sử dụng 1 ẩn phụ để chuyển phương trình mũ ban đầu thành 1 phương trình với 1 ẩn phụ. Khi sử dụng cách giải phương trình mũ này, ta cần thực hiện theo các bước sau:
- Bước 1: Đưa phương trình mũ về dạng ẩn phụ quen thuộc
- Bước 2: Đặt ẩn phụ thích hợp và tìm điều kiện cho ẩn phụ
- Bước 3: Giải phương trình mũ với ẩn phụ mới và tìm nghiệm thỏa mãn điều kiện
- Bước 4: Thay giá trị t tìm được vào giải phương trình mũ cơ bản
- Bước 5: Kết luận
Các phép ẩn phụ giải phương trình mũ và logarit thường gặp như sau:
Dạng 1: Các số hạn trong phương trình mũ có thể biểu diễn qua $a^{f(x)}$ nên ta đặt $t=a^{f(x)}$
Lưu ý trong loại này ta còn gặp một số bài mà sau khi đặt ẩn phụ ta thu được 1 phương trình vẫn chứa x. Khi đó, ta gọi đó là các bài toán đặt ẩn phụ không hoàn toàn.
Dạng 2: Phương trình mũ đẳng cấp bậc n đối với $a^{nf(x)}$ và $b^{nf(x)}$
Với dạng này, ta sẽ chia cả 2 vế của phương trình mũ cho $a^{nf(x)}$ hoặc $b^{nf(x)}$ với n là số tự nhiên lớn nhất có trong phương trình mũ. Sau khi chia ta sẽ đưa được phương trình mũ về dạng 1.
Dạng 3: Trong phương trình có chứa 2 cơ số nghịch đảo
-
Loại 1: $A.a^{f(x)}+B.b^{f(x)}+C=0$ với $a.b=1$
=> Đặt ẩn phụ $t=a^{f(x)}Rightarrow bf(x)=frac{1}{t}$
-
Loại 2: $A.a^{f(x)}+B.b^{f(x)}+C=0$ với $a.b=c^2$
=> Chia 2 vế của phương trình mũ cho $c^{f(x)}$ và đưa về dạng 1.
Ta cùng xét các ví dụ sau để hiểu rõ hơn về cách đặt ẩn phụ giải phương trình mũ và logarit nhé!
Dạng 3: Logarit hoá
Trong một số trường hợp, chúng ta không thể giải phương trình mũ bằng cách đưa về cùng cơ số hoặc dùng ẩn phụ được. Khi đó, các em cần lấy logarit 2 vế theo cùng một cơ số thích hợp nào đó để đưa về dạng phương trình mũ cơ bản. Phương pháp giải phương trình mũ và logarit này được gọi là logarit hoá.
Dấu hiệu nhận biết bài toán phương trình mũ áp dụng phương pháp logarit hóa: Phương trình loại này thường có dạng $a^{f(x)}.b^{g(x)}.c^{h(x)}=d$ (tức là trong phương trình có chứa nhiều cơ số khác nhau và số mũ cũng khác nhau). Khi đó, các em có thể lấy logarit 2 vế theo cơ số a (hoặc b, hoặc c).
Các công thức logarit hoá phương trình mũ như sau:
Sau đây, các em cùng theo dõi ví dụ minh hoạ:
Dạng 4: Sử dụng tính đơn điệu của hàm số giải phương trình mũ
Để sử dụng tính đơn điệu vào trong cách giải phương trình mũ, ta cần nắm vững cách khảo sát hàm số mũ như sau:
-
Tập xác định của hàm số mũ $y=a^x (0<aneq 1)$ là $mathbb{R}$.
-
Chiều biến thiên
-
$a>1$: Hàm số luôn đồng biến
-
$0<a<1$: Hàm số luôn nghịch biến
-
-
Tiệm cận: Trục hoành $Ox$ là đường tiệm cận ngang
-
Đồ thị: Đi qua điểm $(0;1), (1;a)$ và nằm phía trên trục hoành.
Để giải theo phương pháp giải phương trình mũ này, ta cần làm theo các bước sau đây:
Hướng 1:
• Bước 1. Chuyển phương trình về dạng $f(x)=k$.
• Bước 2. Khảo sát sự biến thiên của hàm số $f(x)$ trên $D$. Khẳng định hàm số đơn điệu
• Bước 3. Nhận xét:
+ Với $x=x_0$ ⇔ $f(x)=f(x_0)=k$ do đó $x=x_0$ là nghiệm.
+ Với $x>x_0$ ⇔ $f(x)>f(x_0)=k$ do đó phương trình vô nghiệm.
+ Với $x<x_0$ ⇔ $f(x)<f(x_0)=k$ do đó phương trình vô nghiệm.
• Bước 4. Kết luận vậy $x=x_0$ là nghiệm duy nhất của phương trình.
Hướng 2:
• Bước 1. Chuyển phương trình về dạng $f(x)=g(x)$.
• Bước 2. Khảo sát sự biến thiên của hàm số $y=f(x)$ và $y=g(x)$. Khẳng định hàm số $y=f(x)$ là hàm số đồng biến còn $y = g(x)$ là hàm số nghịch biến hoặc là hàm hằng.
• Bước 3. Xác định $x_0$ sao cho $f(x_0)=g(x_0)$ .
• Bước 4. Kết luận vậy $x=x_0$ là nghiệm duy nhất của phương trình.
Hướng 3:
• Bước 1. Chuyển phương trình về dạng $f(u)=f(v)$.
• Bước 2. Khảo sát sự biến thiên của hàm số $y=f(x)$. Khẳng định hàm số đơn điệu.
• Bước 3. Khi đó $f(u)=f(v)$ ⇔ $u=v$.
Ta xét các ví dụ sau giải phương trình mũ và logarit sử dụng tính đơn điệu:
Dạng 5: Giải phương trình mũ có chứa tham số
Với phương trình có chứa tham số: $f(x;m)=g(m)$, chúng ta thực hiện các bước sau:
Bước 1: Lập luận số nghiệm của (1) là số giao điểm của đồ thị hàm số (C): $y=f(x;m)$ và đường thẳng (d): $y=g(m)$
Bước 2: Xét hàm số $y=f(x;m)$
-
Tìm miền xác định D
-
Tính đạo hàm y’ rồi giải phương trình y’=0
-
Lập bảng biến thiên của hàm số
Bước 3: Kết luận:
-
Phương trình có nghiệm khi và chỉ khi minf(x;m) nhỏ hơn hoặc bằng g(m) nhỏ hơn hoặc bằng $maxf(x;m)$ $(xin mathbb{R})$
-
Phương trình có k nghiệm phân biệt khi và chỉ khi (d) cắt (C) tại K điểm phân biệt.
-
Phương trình vô nghiệm khi và chỉ khi (d) giao (C) bằng rỗng
Ta cùng xét ví dụ giải phương trình mũ logarit sau đây:
2.2. Phương pháp giải phương trình logarit
Dạng 1: Phương pháp đưa về cùng cơ số
Một lưu ý nhỏ cho các em đó là trong quá trình biến đổi để tìm ra cách giải pt logarit, chúng ta thường quên việc kiểm soát miền xác định của phương trình. Vì vậy để cho an toàn thì ngoài phương trình logarit cơ bản, các bạn nên đặt điều kiện xác định cho phương trình trước khi biến đổi.
Phương pháp giải dạng toán này như sau:
Trường hợp 1: $log_af(x)=bRightarrow f(x)=a^b$.
Trường hợp 2: $log_af(x)=log_bg(x)Rightarrow f(x)=g(x)4.
Ta cùng xét ví dụ sau để rõ hơn về cách giải phương trình mũ logarit bằng cách đưa về cùng cơ số:
Dạng 2: Phương pháp đặt ẩn phụ
Ở cách giải phương trình mũ và logarit này, khi đặt ẩn phụ, chúng ta cần chú ý xem miền giá trị của ẩn phụ để đặt điều kiện cho ẩn phụ hoặc không. Ta có công thức tổng quát như sau:
Phương trình dạng: $Q[log_af(x)]=0$ -> Đặt $t=log_ax (xin mathbb{R})$
Các em cùng VUIHOC xét ví dụ sau đây:
Dạng 3: Giải phương trình logarit bằng phương pháp mũ hoá
Bản chất của việc giải phương trình logarit cơ bản (ở trên) cũng là mũ hóa 2 vế với cơ số a. Trong 1 số trường hợp, phương trình có cả loga có cả mũ thì ta có thể thử áp dụng mũ hóa 2 vế để giải.
Phương trình $log_af(x)=log_bg(x) (0<aneq 1)$
Ta đặt $log_af(x)=log_bg(x)=t$ => Hoặc $f(x)=a^t$ hoặc $g(x)=b^t$
=> Đưa về dạng phương trình ẩn $t$.
Dạng 4: Dùng đồ thị giải phương trình logarit
Giải phương trình: $log_ax=f(x) (0<aneq 1)$ (Đây là phương trình hoành độ giao điểm của 2 đồ thị $y=log_ax (0<aneq 1)$ và $y=f(x)$. Khi đó ta thực hiện 2 bước:
-
Bước 1: Vẽ đồ thị các hàm số: $y=log_ax (0<aneq 1)$ và $y=f(x)$
-
Bước 2: Kết luận nghiệm của phương trình đã cho là số giao điểm của đồ thị
Ta có ví dụ minh hoạ về phương pháp giải phương trình logarit này như sau:
3. Bài tập áp dụng cách giải phương trình mũ và logarit
Để thành thạo phân biệt các dạng bài tập áp dụng cách giải phương trình mũ và logarit, VUIHOC gửi tặng các em file bài tập luyện tập giải phương trình mũ và logarit có hướng dẫn giải chi tiết. Các em nhớ tải về theo link dưới đây nhé!
Tải xuống file bài tập giải phương trình mũ và logarit có đáp án
Để luyện tập thành thạo hơn các dạng bài giải phương trình mũ và logarit, thầy Thành Đức Trung có bài giảng về phương trình mũ và phương trình logarit cực hay, trong đó tổng hợp rất nhiều dạng bài thường gặp trong đề thi THPTQG kèm theo các tips giải siêu nhanh. Các em học sinh đừng bỏ qua nhé!
VUIHOC vừa cùng các em ôn tập lại lý thuyết phương trình mũ logarit kèm theo các dạng bài tập giải phương trình mũ và logarit điển hình. Chúc các em ôn tập tốt!
Link nội dung: https://studyenglish.edu.vn/index.php/phuong-trinh-mu-va-logarit-a64665.html