Log Formulas

Before learning log formulas, let us recall what are logs (logarithms). A logarithm is just another way of writing exponents. When we cannot solve a problem using the exponents, then we use logarithms. There are different logarithm formulas that are derived by using the laws of exponents. Let us learn them using a few solved examples.

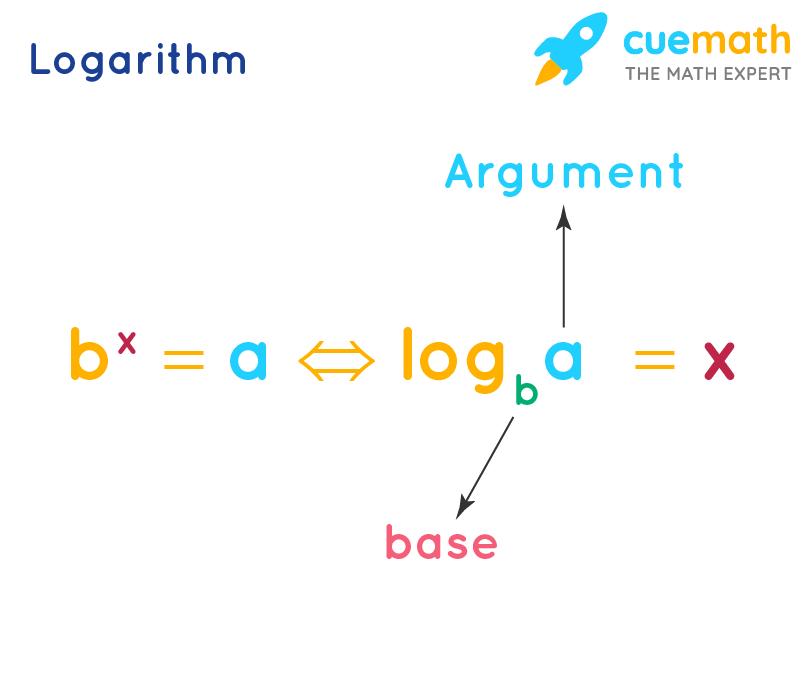
What are Log Formulas?

Before going to learn the log formulas, let us recall a few things. There are two types of logarithms, common logarithm (which is written as "log" and its base is 10 if not mentioned) and natural logarithm (which is written as "ln" and its base is always "e"). The below logarithm formulas are shown for common logarithms. However, they are all applicable for natural logarithms as well. Here are the most commonly used log formulas.

• logb 1 = 0
• logb b = 1
• logb (xy) = logb x + logb y
• logb (x / y) = logb x - logb y
• logb ax = x logb a
• logb a = (logc a) / (logc b)

Some of these rules have specific names like logb (xy) = logb x + logb y is called the product formula of logs. In the same way, all the properties along with their names are mentioned in the table below.

Logarithmic Formulas Derivation

Here is the derivation of some important log formulas. We use the laws of exponents in the derivation of log formulas.

Product Formula of logarithms

The product formula of logs is, logb (xy) = logb x + logb y.

Derivation:

Let us assume that logb x = m and logb y = n. Then by the definition of logarithm,

x = bm and y = bn.

Then xy = bm × bn = bm + n (by a law of exponents, am × an = am + n)

Converting xy = bm + n into logarithmic form, we get

m + n = logb xy

Substituting the values logb x = m and logb y = n here,

logb (xy) = logb x + logb y

Quotient Formula of logarithms

The quotient formula of logs is, logb (x/y) = logb x - logb y.

Derivation:

Let us assume that logb x = m and logb y = n. Then by the definition of logarithm,

x = bm and y = bn.

Then x/y = bm / bn = bm - n (by a law of exponents, am / an = am - n)

Converting x/y = bm - n into logarithmic form, we get

m - n = logb (x/y)

Substituting the values logb x = m and logb y = n here,

logb (x/y) = logb x - logb y

Power Formula of Logarithms

The power formula of logarithms says logb ax = x logb a.

Derivation:

Let logb a = m. Then by the definition of logarithm, a = bm.

Raising both sides by x, we get

ax = (bm)x

ax = bmx (by a law of exponents, (am)n = amn)

Converting this back into logarithmic form,

logb ax = m x

Substitute m = logb a here,

logb ax = x logb a

Change of Base Formula of Logarithms

The change of base formula of logs says logb a = (logc a) / (logc b).

Derivation:

Assume that logb a = x, logc a = y, and logc b = z.

Converting these into exponential forms,

a = bx ... (1)

a = cy ... (2)

b = cz ... (3)

From (1) and (2),

bx = cy

(cz)x = cy (from (3))

czx = cy

Since the bases are the same, the powers also should be the same.

zx = y (or) x = y / z.

Substituting the values of x, y, and z here back,

logb a = (logc a) / (logc b).

Examples Using Logarithm Formulas

Example 1: Convert the following from exponential form to logarithmic form using the log formulas. a) 53 = 125 b) 3-3 = 1 / 27.

Solution:

Using the definition of the logarithm,

bx = a ⇒ logb a = x

Using this,

a) 53 = 125 ⇒ log5 125 = 3

b) 3-3 = 1 / 27 ⇒ log3 1/27 = -3

Answer: a) log5 125 = 3; b) log3 1/27 = -3.

Example 2: Compress the following expression as a single logarithm by using logarithmic formulas. 5 log x + log y - 8 log z.

Solution:

To find: The compressed form of the given expression as a single logarithm using logarithm formulas.

5 log x + log y - 8 log z

= (5 log x - 8 log z) + log y (Regrouped the terms)

= (log x5 - log z8) + log y (∵ a log x = log xa)

= log (x5/z8) + log y (∵ log x - log y = log (x/y) )

= log (x5y/z8) (∵ log x + log y = log (xy) )

Answer: 5 log x + log y - 8 log z = log (x5y/z8).

Example 3: Find the integer value of log3 (1/9) using log formulas.

Solution:

log3 (1/9) = log3 1 - log3 9 (∵ logb (x / y) = logb x - logb y)

= 0 - log3 32 (∵ logb 1 = 0)

= - 2 log3 3 (∵ logb ax = x logb a)

= -2 (1) (∵ logb b = 1)

= -2

Answer: log3 (1/9) = -2.