
Con lắc đơn dao động điều hòa, vật lí 11
Lý thuyết dao động điều hòa, năng lượng dao động, lực căng dây của con lắc đơn, vật lí 11 DAO ĐỘNG

Dao động của con lắc đơn:
Kéo vật m sao cho dây treo hợp với phương thẳng đứng góc α rồi buông tay, Dưới tác dụng của trọng lực vật m chuyển động về vị trí cân bằng ban đầu (là vị trí góc α=0o), khi đến vị trí cân bằng do quán tính vật m tiếp tục chuyển động sang trái, nếu bỏ qua sức cản của không khí vật sẽ chuyển động đến vị trí sao cho dây treo hợp với phương thẳng đứng một góc α. Tại đó vật m dừng lại và chuyển động ngược trở lại vị trí cân bằng, chuyển động trên được lặp đi lặp lại => vật m dao động xung quanh vị trí cân bằng
Bài giảng về dao động điều hòa của con lắc đơn
Điều kiện để con lắc đơn dao động điều hòa
Gọi độ dài quãng đường mà vật m chuyển động từ vị trí góc hợp bởi dây treo và phương thẳng đứng góc α về vị trí cân bằng (α = 0) là s.
Với góc α đủ nhỏ (α ≤ 10o) ta có [tex]alpha approx sinalpha=dfrac{s}{ell}[/tex]
Bài giảng về lực căng dây, năng lượng dao động
Năng lượng dao động của con lắc đơn
b/ Thế năng:
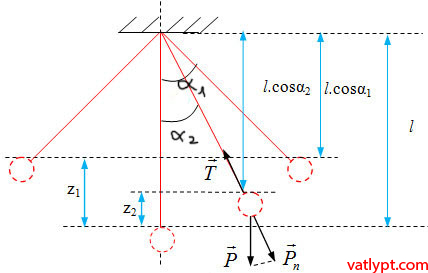
Chọn gốc thế năng tại vị trí cân bằng (α=0o),
Lực căng của dây
Chuyển động của vật m là chuyển động tròn đều trên bán kính quỹ đạo có bán kính l, hợp giữa lực căng T của dây treo và thành phần P$_{n }$ = mgcosα của trọng lực đóng vai trò lực hướng tâm => áp dụng định luật II Newton ta có
T - mgcosα=m.[tex]frac{v^{2}}{l}[/tex]=>
T=mgcosα + 2mg(cosα - cosαo) =>
Bài tập vận dụng
Bài tập 1. Một con lắc đươn treo một vật nặng khối lượng 100g, chiều dài dây treo 1m, treo tại nơi có g = 9,86m/s2. Bỏ qua mọi ma sát. Kéo con lắc lệch khỏi vị trí cân bằng góc αo rồi thả không vận tốc đầu. Biết con lắc dao động điều hòa với năng lượng W = 8.10-4(J). Viết phương trình dao động điều hòa của con lắc, chọn gốc thời gian lúc vật nặng có li độ cực đại dương, lấy π2 = 10
A. s = 4cos(πt + π) cm
B. s = 4√2cos(πt + π) cm
C. s = 4√2 cos(πt + π/2)cm
D. s = 4cos(πt) cm
Bài tập 2. Một con lắc đơn có chiều dài l = 40cm, được treo tại nơi có g = 10m/s2. Bỏ qua sức cản không khí. Đưa con lắc lệch khỏi vị trí cân bằng một góc 0,1rad rồi truyền cho vật nặng vận tốc 20cm/s theo phương vuông góc với dây hướng về vị trí cân bằng. chọn gốc tọa độ tại vị trí cân bằng của vật nặng, gốc thời gian là lúc vật nặng tiếp tuyến với quỹ đạo lần thứ nhất. Viết phương trình dao động của con lắc theo li độ cong.
A. s = 8cos(5t + π)cm
B. s = 4√2cos(5t + π)cm
C. s = 4√2cos(5t + π/2)
D. s = 8cos(25t)
Bài tập 3. Một con lắc đơn dài l = 20cm treo tại một điểm cố định, Kéo con lắc khỏi phương thẳng đứng một góc bằng 0,1rad về phía bên phải rồi truyền cho vật vận tốc 14cms theo phương vuôg góc với dây về phía vị trí cân bằng. Coi con lắc dao động điều hòa. Viết phương trình dao động đối với li độ dài của con lắc. Chọn gốc tọa độ tại vị trí cân bằng chiều dương hướng từ vị trí cân bằng sang phải, gốc thời gian là lúc con lắc qua vị trí cân bằng lần thứ nhất. lấy g = 9,8m/s2
A. s = 2√2cos(7πt + π/2)cm
B. s = 2√2cos(5πt + π/4)cm
C. s = 2√2cos(5t - π/4)cm
D. s = 2√2cos(7t + π/2)cm
Bài tập 4. Một con lắ đơn đang nằm yên tại vị trí cân bằng, truyền cho nó một vận tốc vo = 40cm/s theo phương ngang thì con lắc đươn dao động điều hòa. Biết rằng tại vị trí có li độ góc α = 0,1√3 rad thì nó có vận tốc v = 20cm/s. Lấy g = 10m/s2. chọn gốc thời gian là lúc truyền vận tốc cho vật, chiều dương cùng chiều với vận tốc ban đầu. Viết phương trình dao động của con lắc theo li độ dài
A. s = 8cos(5πt + π/2)cm
B. s = 8√2cos(5πt - π/4)cm
C. s = 8√2cos(5πt + π/4)cm
D. s = 8cos(5t - π/2)cm
Link nội dung: https://studyenglish.edu.vn/index.php/dieu-kien-de-con-lac-don-dao-dong-dieu-hoa-a70864.html