
Bài tập Toán 12 Giải tích câu hỏi ôn tập cuối năm
Giải bài tập Toán 12 câu hỏi ôn tập
VnDoc.com xin giới thiệu tới bạn đọc tài liệu: Bài tập Toán 12 Giải tích câu hỏi ôn tập cuối năm, với bộ câu hỏi kèm theo lời giải chi tiết sẽ giúp các bạn học sinh giải nhanh các bài tập Toán một cách hiệu quả. Mời các bạn và thầy cô tham khảo.
Bài tập Toán 12 Giải tích câu hỏi ôn tập cuối năm
Câu hỏi 1 (trang 145 SGK Giải tích 12): Định nghĩa sự đơn điệu (đồng biến, nghịch biến) của một hàm số trên một khoảng.
Lời giải:
Cho hàm số y = f(x) xác định trên K, hàm số f(x):
Đồng biến (tăng) trên K nếu ∀ x1, x2 ∈ K: x1 < x2 => f(x1) < f(x2).
Nghịch biến ( giảm) trên K nếu ∀ x1, x2 ∈: x1 < x2 => f(x1) > f(x2)
Hàm số đồng biến hay nghịch biến trên K gọi là đơn điệu trên K.
Câu hỏi 2 (trang 145 SGK Giải tích 12): Phát biểu các điều kiện cần và đủ để hàm số f(x) đơn điệu trên một khoảng.
Lời giải:
Cho hàm số y = f(x) có đạo hàm trên K
Nếu f’(x) > 0, x ∈ K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số thì f(x) đồng biến trên K.
Nếu f’(x) < 0, x ∈ K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số f(x) nghịch biến trên K.
Câu hỏi 3 (trang 145 SGK Giải tích 12): Phát biểu các điều kiện đủ để hàm số f(x) có cực trị (cực đại cực tiểu) tại điểm xo
Lời giải:
Điều kiện để hàm có cực trị:
Định lí 1: Cho hàm số y = f(x) liên tục trên K = (x0 - h; x0 + h), h > 0 và có đạo hàm trên K hoặc trên K {x0}, nếu:
- f’(x) > 0 trên (x0 - h; x0) và f’(x) < 0 trên (x0; x0 + h) thì x0 là một điểm cực đại của f(x).
- f’(x) < 0 trên (x0 - h; x0) và f’(x) > 0 trên (x0; x0 + h) thì x0 là một điểm cực tiểu của f(x).
Câu hỏi 4 (trang 145 SGK Giải tích 12): Nêu sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số.
Lời giải:
Bước 1: Tìm tập xác định của hàm số
Bước 2: Xét sự biến thiên
- Xét chiều biến thiên:
+ Tìm đạo hàm f’(x)
+ Tìm các điểm mà tại đó f’(x) bằng không hoặc không xác định
+ Xét dấu của đạo hàm f’(x) và suy ra chiều biến thiên của hàm số.
- Tìm cực trị
- Tìm giới hạn vô cực và tiệm cận ( nếu có)
- Lập bảng biến thiên.
Bước 3: Vẽ đồ thị hàm số.
Câu hỏi 5 (trang 145 SGK Giải tích 12): Nêu định nghĩa và các tính chất cơ bản của loogarit.
Lời giải:
Câu hỏi 6 (trang 145 SGK Giải tích 12): Phát biểu định lí về quy tắc logarit, công thức đổi cơ số.
Lời giải

Câu hỏi 7 (trang 145 SGK Giải tích 12): Nêu tính chất của hàm số mũ, hàm số logarit, mối liên hệ giữa đồ thị của hàm số mũ cà hàm số logarit cùng cơ số.
Lời giải:
1. Hàm số mũ
Cho số a > 0, a ≠ 1. Hàm số y = ax được gọi là hàm số mũ cơ số a.
Khảo sát:
* D = R.
* Nếu:
- a > 1: hàm số luôn đồng biến
- 0 < a < 1: hàm số luôn nghịch biến
* Đồ thị luôn đi qua hai điểm ( 0; 1) và (1; a) có tiệm cận ngang là trục Ox.
2. Hàm Logarit
Cho số a > 0, a ≠ 1 . Hàm số 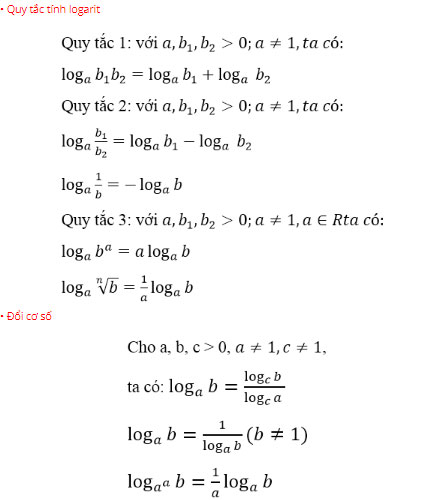 được gọi là hàm logarit cơ số a.
được gọi là hàm logarit cơ số a.
Khảo sát:
* D = (0;+∞)
* Nếu:
- a > 1: Hàm số luôn đồng biến trên D
- 0 < a < 1: hàm số luôn nghịch biến
* Đồ thị luôn đi qua hai điểm (1; 0) và (a; 1) có tiệm cận đứng là trục Oy.
• Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.
Câu hỏi 8 (trang 145 SGK Giải tích 12): Nêu định nghĩa và các phương pháp tính nguyên hàm.
Lời giải:
Nguyên hàm
Cho hàm số f(x) xác định trên K (k là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K.
Phương pháp tính nguyên hàm
Đổi biến số:
Câu hỏi 9 (trang 145 SGK Giải tích 12): Nêu định nghĩa và các phương pháp tính tích phân.
Lời giải:
• Định nghĩa
Cho hàm số y = f(x) liên tục trên [a; b], F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) - F(a) được gọi là tích phân từ a đến b của hàm số f(x)
Câu hỏi 10 (trang 145 SGK Giải tích 12): Nhắc lại định nghĩa số phức, số phức liên hợp, mô đun của số phức. Biểu diễn hình học của số phức.
Lời giải:
1. Số phức
Mỗi biểu thức dạng a + bi, trong đó: a, b ∈ R;i2= -1 được gọi là số phức. Trong đó a được gọi là phần thực, b gọi là phần ảo, số i là đơn vị ảo.
2. Mô đun
Cho số phức z = a + bi, được biểu diễn bởi điểm M(a;b) trên tọa độ Oxy. Ta gọi mô đun của số phức z, kí hiệu là |z| là đọ dài của vectơ OM.
Link nội dung: https://studyenglish.edu.vn/index.php/on-tap-cuoi-nam-toan-12-a71277.html
