Giải Toán 8 bài 3: Hình thang cân được VnDoc tổng hợp và chia sẻ. Lời giải Toán 8 tổng hợp đáp án cho các câu hỏi trong SGK Toán 8 tập 1 trang 72, 74, 75. Hy vọng với tài liệu này sẽ giúp ích cho các em học sinh tham khảo, so sánh đáp án, từ đó học tốt môn Toán lớp 8. Dưới đây là nội dung chi tiết, mời các em tham khảo.
A. Trả lời câu hỏi trang 72, 74 SGK Toán 8 tập 1
Câu hỏi 1 trang 72 SGK Toán 8 tập 1
Hình thang ABCD (AB // CD) trên hình 23 có gì đặc biệt?
Lời giải
Hình thang ABCD trên hình 23 có hai góc kề cạnh đáy lớn bằng nhau
Câu hỏi 2 trang 72 SGK Toán 8 tập 1
Cho hình 24.
a) Tìm các hình thang cân.
b) Tính các góc còn lại của mỗi hình thang cân đó.
c) Có nhận xét gì về hai góc đối của hình thang cân?
Lời giải
a) Các hình thang cân là: ABDC, IKMN, PQST
b) Áp dụng định lí tổng các góc của một tứ giác bằng 3600
⇒ góc 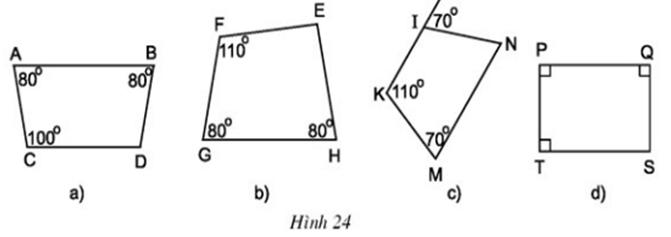 (D=360^{circ}-80^{circ}-80^{circ}-100^{circ}=100^{circ})
(D=360^{circ}-80^{circ}-80^{circ}-100^{circ}=100^{circ})
Góc N = 70o(so le trong với góc 70o)
Góc (S=360^{circ}-90^{circ}-90^{circ}-90^{circ}=90^{circ})
c) Hai góc đối của hình thang cân bù nhau
Câu hỏi 3 trang 74 SGK Toán 8 tập 1
Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc C và D của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.
Lời giải
Hai góc C và D bằng nhau
⇒ Hình thang có hai đường chéo bằng nhau là hình thang cân
B. Giải Toán 8 tập 1 bài 3 trang 74
Bài 11 trang 74 sgk Toán 8 tập 1
Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).
Lời giải:
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm.
Áp dụng định lí Pitago trong tam giác vuông AED ta được:
AD2 = AE2 + ED2 = 32 + 12 = 10.
Suy ra  (AD=sqrt{10}cm)
(AD=sqrt{10}cm)
Vậy AB = 2cm, CD = 4cm,  (AD=BC=sqrt{10}cm)
(AD=BC=sqrt{10}cm)
Bài 12 trang 74 sgk Toán 8 tập 1
Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
Lời giải:
Vì hình thang ABCD cân
AD = BC;
(widehat C = widehat D)
Xét hai tam giác vuông AED và BFC có:
AD = BC
(widehat C = widehat D)
⇒ ΔAED = ΔBFC (cạnh huyền - góc nhọn)
⇒ DE = CF.
Bài 13 trang 74 sgk Toán 8 tập 1
Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Lời giải:
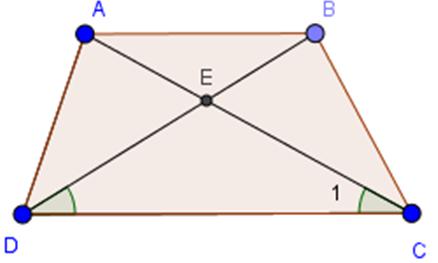
Xét hai tam giác ADC và BCD có:
AD = BC (ABCD là hình thang cân)
AC = BD (hai đường chéo của hình thang cân)
DC chung
Nên 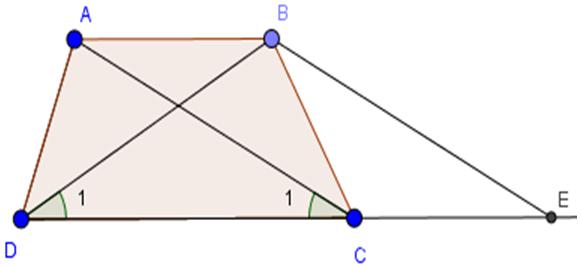 (Delta ADC = Delta BCD (c-c-c))
(Delta ADC = Delta BCD (c-c-c))
Suy ra(widehat{ACD} = widehat{BDC})
Do đó 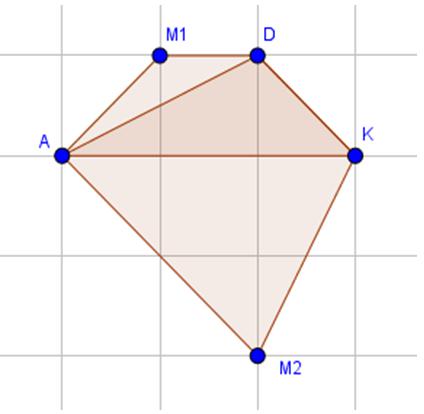 (Delta DEC) cân tại E
(Delta DEC) cân tại E
Suy ra EC = ED
Mặt khác AC = BD nên EA = EB
Bài 14 trang 75 sgk Toán 8 tập 1
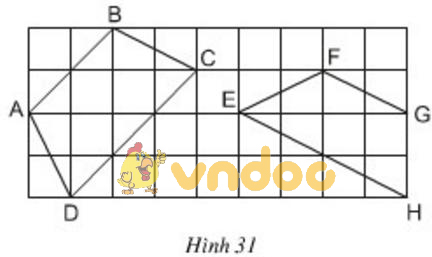
Đố. Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?
Lời giải:
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất "Trong hình thang cân hai cạnh bên bằng nhau".
Tứ giác ABCD là hình thang cân vì AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Giải bài tập Toán 8 trang 75 tập 1: Luyện tập
Bài 15 trang 75 sgk Toán 8 tập 1
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50o.
Lời giải:
Ta có: AD = AE
=> Tam giác ADE cân
=> (widehat {{D_1}} = widehat {{E_1}})
Xét tam giác ADE có:
(begin{matrix} widehat A + widehat {{D_1}} + widehat {{E_1}} = {180^0} hfill widehat {{D_1}} = widehat {{E_1}} Rightarrow widehat A + 2.widehat {{D_1}} = {180^0} hfill Rightarrow 2.widehat {{D_1}} = {180^0} - widehat A Rightarrow widehat {{D_1}} = dfrac{{{{180}^0} - widehat A}}{2}left( * right) hfill end{matrix})
Xét tam giác ABC có:
(begin{matrix} widehat A + widehat B + widehat C = {180^0} hfill widehat B = widehat C hfill Rightarrow widehat A + 2.widehat B = {180^0} hfill Rightarrow 2.widehat B = {180^0} - widehat A Rightarrow widehat B = dfrac{{{{180}^0} - widehat A}}{2}left( {**} right) hfill end{matrix})
Từ (*) và (**) (Rightarrow widehat {{D_1}} = widehat B)
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b) Ta có: (widehat A = {50^0})
Thay vào (**)
(begin{matrix} Rightarrow widehat B = dfrac{{{{180}^0} - {{50}^0}}}{2} = {65^0} hfill widehat B = widehat C hfill Rightarrow widehat C = {65^0} hfill {text{Do DE // BC }} hfill Rightarrow widehat {{D_2}} + widehat B = {180^0} Rightarrow widehat {{D_2}} = {180^0} - widehat B = {115^0} hfill end{matrix})
Mặt khác DECB là hình thang cân
Bài 16 trang 75 sgk Toán 8 tập 1
Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Lời giải:
Ta có:
(widehat{ABD} = frac{1}{2}widehat{B}) (BD là phân giác)
(widehat{ACE} = frac{1}{2}widehat{C}) (CE là phân giác)
Mà (widehat{B} = widehat{C}) (tam giác ABC cân tại A)
Nên (widehat{ABD} = widehat{ACE})
Xét hai tam giác ADB và AEC có:
(widehat{A}) chung
AB = AC (tam giác ABC cân tại A)
(widehat{ABD} = widehat{ACE}) (chứng minh trên)
Do đó (Delta ADB = Delta AEC (g-c-g))
Suy ra AD = AE
Nên tam giác ADE cân tại A
Ta có:
(widehat{AED} = frac{180^0 - widehat{A}}{2}) (tam giác ADE cân tại A)
(widehat{B} = frac{180^0 - widehat{A}}{2}) (tam giác ABC cân tại A)
Suy ra (widehat{AED} = widehat{B})
Nên ED // BC
Do đó: tứ giác BEDC là hình thang
Hình thang BEDC có (widehat{B} = widehat{C}) nên BEDC là hình thang cân.
Ta có (ED//BC ⇒ widehat{D_1} = widehat{B_2}) (so le trong)
Mà (widehat{B_1} = widehat{B_2}) (chứng minh trên)
Nên (widehat{D_1} = widehat{B_1})
Do đó tam giác BED cân tại E
Suy ra EB = ED
Vậy hình thang BEDC là hình thang cân có đáy nhỏ ED bằng cạnh bên EB.
Bài 17 trang 75 sgk Toán 8 tập 1
Hình thang ABCD (AB//CD) có (widehat{ACD} = widehat{BDC}) . Chứng minh rằng ABCD là hình thang cân.
Lời giải:
Ta có
(widehat{ACD} = widehat{BDC}) nên tam giác DEC cân tại E
Suy ra ED = EC (1)
Ta lại có: (AB // CD ⇒ begin{cases}widehat{ACD} = widehat{BAE}widehat{BDC} = widehat{ABE}end{cases})
Mà (widehat{ACD} = widehat{BDC} (gt))
Nên (widehat{BAE} = widehat{ABE})
Do đó tam giác AEB cân tại A ⇒ EA = EB (2)
Từ (1) và (2) suy ra: AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên ABCD là hình thang cân.
Bài 18 trang 75 sgk Toán 8 tập 1
Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:
a) ΔBDE là tam giác cân.
b) ΔACD = ΔBDC
c) Hình thang ABCD là hình thang cân.
Lời giải:
a. Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
AC = BD (gt) (2)
Từ (1) và (2) suy ra BE = BD
=> ΔBDE cân
b. Do AC // BE nên (widehat E = widehat {{C_1}}) (3)
Mà ΔBDE cân tại B nên (widehat E = widehat {{D_1}})(4)
Từ (3) và (4) => (widehat {{C_1}} = widehat {{D_1}})
Xét ΔACD và ΔBDC có:
DC chung
AC = BD (gt)
(widehat {{C_1}} = widehat {{D_1}}) (cmt)
=> ΔACD = ΔBDC (c - g - c)
Ta có ΔACD = ΔBDC => (widehat {ADC} = widehat {BCD}) (hai góc tương ứng)
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài 19 trang 75 sgk Toán 8 tập 1
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32) Hãy tìm điểm thứ tư M giao điểm của các dòng kẻ sao cho nó cùng với ba diểm đã cho là bốn đỉnh của một hình thang cân.
Lời giải:
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình ADKM2(với DK là đáy).
Như vậy là VnDoc đã hướng dẫ tới các em học sinh bài Giải Toán 8 bài 3: Hình thang cân. Nội dung gồm 11 câu hỏi tương ứng các bài tập nằm trong SGK lớp 8 bài 3. Hy vọng với lời giải chi tiết sẽ giúp các em nắm chắc kiến thức, áp dụng tốt vào giải bài tập Toán 8. Chúc các em học tốt, nếu thấy hay hãy chia sẻ cho các bạn cùng biết nhé
..............................
Bài tiếp theo: Giải Toán 8 bài 4: Đường trung bình của tam giác, của hình thang
Xem thêm:
- Toán 8 Bài 3: Hình thang cân
- Giải bài tập SBT Toán 8 bài 3: Hình thang cân
- Chuyên đề Toán 8: Hình thang cân
Trên đây, VnDoc đã gửi tới các bạn tài liệu Giải Toán 8 bài 3: Hình thang cân. Để tham khảo lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải Toán lớp 8 theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong từng bài, từ đó học tốt Toán 8 hơn.
Ngoài Soạn Toán 8, mời các bạn tham khảo thêm Giải SBT Toán 8, Giải Vở BT Toán 8 và các đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa... được cập nhật liên tục trên VnDoc.


