VIẾT BIỂU THỨC CỦA u HOẶC i
I.ĐOẠN MẠCH CHỈ CÓ 1 PHẦN TỬ:
a) Đoạn mạch chỉ có điện trở thuần:
uR cùng pha với i : I = (frac{U_{R}}{R})
b) Đoạn mạch chỉ có tụ điện C:
uC trễ pha so với i góc (frac{pi }{2}).
- ĐL ôm: I = (frac{U_{C}}{Z_{C}}) ; với ZC = (frac{1}{omega C}) là dung kháng của tụ điện.
-Đặt điện áp (u=Usqrt{2}cosomega t) vào hai đầu một tụ điện thì cường độ dòng điện qua nó có giá trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu tụ điện là u và cường độ dòng điện qua nó là i. Hệ thức liên hệ giữa các đại lượng là :
Ta có:({left( {{i over {{I_0}}}} right)^2} + {left( {{u over {{U_{0C}}}}} right)^2} = 1 Leftrightarrow {rm{ }}{{{i^2}} over {2{I^2}}}{rm{ }} + {{{u^2}} over {2{U_C}^2}} = 1 Rightarrow {{{u^2}} over {{U^2}}} + {{{i^2}} over {{I^2}}} = 2)
-Cường độ dòng điện tức thời qua tụ: (i=Isqrt{2}cos(omega t+frac{pi }{2}))
c) Đoạn mạch chỉ có cuộn dây thuần cảm L:
uL sớm pha hơn i góc (frac{pi }{2}) .
- ĐL ôm: I = (frac{U_{L}}{Z_{L}}); với ZL = ωL là cảm kháng của cuộn dây.
-Đặt điện áp (u=Usqrt{2}cosomega t) vào hai đầu một cuộn cảm thuần thì cường độ dòng điện qua nó có giá
trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu cuộn cảm thuần là u và cường độ dòng điện
qua nó là i. Hệ thức liên hệ giữa các đại lượng là :
Ta có: ({left( {{i over {{I_0}}}} right)^2} + {left( {{u over {{U_{0L}}}}} right)^2} = 1 Leftrightarrow {{{i^2}} over {2{I^2}}}{rm{ }} + {{{u^2}} over {2{U_L}^2}} = 1 Rightarrow {{{u^2}} over {{U^2}}} + {{{i^2}} over {{I^2}}} = 2)
-Cường độ dòng điện tức thời qua cuộn dây:(i=Isqrt{2}cos(omega t-frac{pi }{2}))
d) Đoạn mạch có R, L, C không phân nhánh:
+Đặt điện áp (u=Usqrt{2}cos(omega t +varphi _{u})) vào hai đầu mạch
+ Độ lệch pha φ giữa u và i xác định theo biểu thức:
(tanvarphi =frac{Z_{L}-Z_{C}}{R}=frac{omega L-frac{1}{omega C}}{R}); Với (varphi =varphi _{u}-varphi _{i})
+ Cường độ hiệu dụng xác định theo định luật Ôm: I = (frac{U}{Z}).
Với Z = (sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}) là tổng trở của đoạn mạch.
Cường độ dòng điện tức thời qua mạch: (i=Isqrt{2}cos(omega t+varphi _{i})=Isqrt{2}cos(omega t+varphi _{u}-varphi ))
+ Cộng hưởng điện trong đoạn mạch RLC: Khi ZL = ZC hay (omega =frac{1}{sqrt{LC}}) thì
Imax = (frac{U}{R},P_{max}=frac{U^{2}}{R}) , Pmax = , u cùng pha với i (φ = 0).
Khi ZL > ZC thì u nhanh pha hơn i (đoạn mạch có tính cảm kháng).
Khi ZL < ZC thì u trể pha hơn i (đoạn mạch có tính dung kháng).
R tiêu thụ năng lượng dưới dạng toả nhiệt, ZL và ZC không tiêu thụ năng lượng điện.
e) Đoạn mạch có R, L,r, C không phân nhánh:
+Đặt điện áp (u=Usqrt{2}cos(omega t +varphi _{u})) vào hai đầu mạch
+ Độ lệch pha φ giữa u và i xác định theo biểu thức:
(tanvarphi =frac{Z_{L}-Z_{C}}{R}=frac{omega L-frac{1}{omega C}}{R}); Với (varphi =varphi _{u}-varphi _{i})
+ Cường độ hiệu dụng xác định theo định luật Ôm: I = (frac{U}{Z}).
Với Z = (sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}) là tổng trở của đoạn mạch.
Cường độ dòng điện tức thời qua mạch: (i=Isqrt{2}cos(omega t+varphi _{i})=Isqrt{2}cos(omega t+varphi _{u}-varphi ))
+ Cách nhận biết cuộn dây có điện trở thuần r
-Xét toàn mạch, nếu: (Zneq sqrt{R^{2}+(Z_{L}-Z_{C})^{2}};Uneq sqrt{U_{R}^{2}+(U_{L}-U_{C})^{2}})
hoặc P ≠ I2R hoặc cosφ ≠ (frac{R}{Z})
à thì cuộn dây có điện trở thuần r ≠ 0.
-Xét cuộn dây, nếu: Ud ≠ UL hoặc Zd ≠ ZL hoặc Pd ≠ 0 hoặc cosφd ≠ 0 hoặc φd ≠ (frac{pi }{2})
=> thì cuộn dây có điện trở thuần r ≠ 0.
II. PHƯƠNG PHÁP 1: (PHƯƠNG PHÁP TRUYỀN THỐNG):
a) Mạch điện chỉ chứa một phần tử ( hoặc R, hoặc L, hoặc C)
- Mạch điện chỉ có điện trở thuần: u và i cùng pha: φ =φu - φi = 0 Hay φu = φi
+ Ta có: (i=Isqrt{2}cos(omega t+varphi _{i})) thì (u=U_{R}sqrt{2}cos(omega t+varphi )) ; với (I=frac{U_{R}}{R}).
+Ví dụ 1: Điện áp giữa hai đầu một đoạn mạch điện xoay chiều chỉ có điện trở thuần R= 100Ω có biểu thức u= (200sqrt{2}cos(100pi t+frac{pi }{4})(V)). Biểu thức của cường độ dòng điện trong mạch là :
A. i=(2sqrt{2}cos(100pi t-frac{pi }{4})(A)) C.i=(2sqrt{2}cos(100pi + frac{pi }{4})(A))
B. i=(2sqrt{2}cos(100pi t+frac{pi }{2})(A)) D.i=(2cos(100pi t-frac{pi }{2})(A))
+Giải :Tính I0 hoặc I= U /.R =200/100 =2A; i cùng pha với u hai đầu R, nên ta có:φi = φu = π/4
Suy ra: i = (2sqrt{2}cos(100pi + frac{pi }{4})(A))
=> Chọn C
-Mạch điện chỉ có tụ điện:
uC trễ pha so với i góc (frac{pi }{2}) . -> φ= φu - φi =- (frac{pi }{2}) Hay φu = φi - (frac{pi }{2}) ; φi = φu +(frac{pi }{2})
+Nếu đề cho (i=Isqrt{2}cos(omega t)) thì viết: (u=Usqrt{2}cos(100pi t-frac{pi }{2})(A)) và ĐL Ôm:(I=frac{U_{C}}{Z_{C}}) với (Z_{C}=frac{1}{omega C})
+Nếu đề cho (u=Usqrt{2}cos(omega t)) thì viết: (i=Isqrt{2}cos(100pi t+frac{pi }{2})(A))
+Ví dụ 2: Điện áp giữa hai đầu một đoạn mạch điện xoay chiều chỉ có tụ có điện dung C= (frac{10^{-4}}{pi }(F)) có biểu thức u=(200sqrt{2}cos(100pi t)(V)). Biểu thức của cường độ dòng điện trong mạch là :
A. i= (2sqrt{2}cos(100pi t+frac{5pi }{6})(A)) C.i=(2sqrt{2}cos(100pi t+frac{pi }{2})(A))
B. i= (2sqrt{2}cos(100pi t-frac{pi }{2})(A)) D.i=(2cos(100pi t-frac{pi }{6})(A))
Giải : Tính (Z_{C}=frac{1}{omega C}=100Omega) , Tính Io hoặc I= U /.ZL =200/100 =2A;
i sớm pha góc π/2 so với u hai đầu tụ điện; Suy ra: i=(2sqrt{2}cos(100pi t+frac{pi }{2})(A))
=> Chọn C
-Mạch điện chỉ có cuộn cảm thuần:
uL sớm pha hơn i góc (frac{pi }{2}) . -> φ= φu - φi =- (frac{pi }{2}) Hay φu = φi + (frac{pi }{2}) ; φi = φu - (frac{pi }{2})
+Nếu đề cho (i=Isqrt{2}cos(omega t)) thì viết: (u=Usqrt{2}cos(100pi t+frac{pi }{2})(A)) và ĐL Ôm: (I=frac{U_{L}}{Z_{L}}) với (Z_{L}=omega L)
Nếu đề cho (u=Usqrt{2}cos(omega t)) thì viết: (i=Isqrt{2}cos(100pi t-frac{pi }{2})(A))
Ví dụ 3: Hiệu điện thế giữa hai đầu một đoạn mạch điện xoay chiều chỉ có cuộn cảm có độ tự cảm L= (frac{1}{pi }(H)) có biểu thức u=(200sqrt{2}cos(100pi t+frac{pi }{3})(V)). Biểu thức cường độ dòng điện trong mạch là :
A. i= (2sqrt{2}cos(100pi t+frac{5pi }{6})(A)) C.i=(2sqrt{2}cos(100pi t-frac{pi }{6})(A))
B. i=(2sqrt{2}cos(100pi t+frac{pi }{6})(A)) D.i=(2cos(100pi t-frac{pi }{6})(A))
Giải : Tính (Z_{L}=omega L) = 100π.1/π =100Ω, Tính I0 hoặc I= U /.ZL =200/100 =2A;
i trễ pha góc π/2 so với u hai đầu cuộn cảm thuần, nên ta có: (frac{pi }{3}-frac{pi }{2}=-frac{pi }{6})
Suy ra: i = (2sqrt{2}cos(100pi t-frac{pi }{6})(A))
=> Chọn C
II.MẠCH ĐIỆN KHÔNG PHÂN NHÁNH (R L C)
a. Phương pháp truyền thống):
-Phương pháp giải: Tìm Z, I ( hoặc I0 )và φ
Bước 1: Tính tổng trở Z: Tính (Z_{L}=omega L) ; (Z_{C}=frac{1}{omega C}=frac{1}{2pi fC}) và (Z=sqrt{R^{2}+(Z_{L}-Z_{C})^{2}})
Bước 2: Định luật Ôm : U và I liên hệ với nhau bởi ; I= (frac{U}{Z}) Io = (frac{U_{0}}{Z});
Bước 3: Tính độ lệch pha giữa u hai đầu mạch và i: (tanvarphi =frac{Z_{L}-Z_{C}}{R});
Bước 4: Viết biểu thức u hoặc i
-Nếu cho trước:(i=Isqrt{2}cos(omega t)) thì biểu thức của u là (u=Usqrt{2}cos(omega t+varphi ))
Hay i = Iocosωt thì u = Uocos(ωt + φ).
-Nếu cho trước: (u=Usqrt{2}cos(omega t)) thì biểu thức của i là: (i=Isqrt{2}cos(omega t-varphi ))
Hay u = Uocosωt thì i = Iocos(ωt - φ)
* Khi: (φu ≠ 0; φ i ≠ 0 ) Ta có : φ = φu - φ i => φu = φi + φ ; φi = φu - φ
-Nếu cho trước (i=Isqrt{2}cos(omega t+varphi_{i} )) thì biểu thức của u là: (u=Usqrt{2}cos(omega t+varphi_{i} +varphi ))
Hay i = Iocos(ωt + φi) thì u = Uocos(ωt + φi + φ).
-Nếu cho trước (u=Usqrt{2}cos(omega t+varphi_{u} ))thì biểu thức của i là: (i=Isqrt{2}cos(omega t+varphi_{u}-varphi ))
Hay u = Uocos(ωt +φu) thì i = Iocos(ωt +φu - φ)
Lưu ý: Với Mạch điện không phân nhánh có cuộn dây không cảm thuần (R ,L,r, C) thì:
Tổng trở :(Z=sqrt{(R+r)^{2}+(Z_{L}-Z_{C})^{2}}) và (tanvarphi =frac{Z_{L}-Z_{C}}{R+r});
Ví dụ 1: Mạch điện xoay chiều gồm một điện trở thuần R = 50Ω, một cuộn thuần cảm có hệ số tự cảm (L=frac{1}{pi }(H)) và một tụ điện có điện dung (C=frac{2.10^{-4}}{pi }(F)) mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng (i=5cos100pi t(A)) .Viết biểu thức điện áp tức thời giữa hai đầu mạch điện.
Giải :
Bước 1: Cảm kháng: (Z_{L}=omega L=100pi .frac{1}{pi }=100Omega ;); Dung kháng: (Z_{C}=frac{1}{omega C}=frac{1}{100pi .frac{2.10^{-4}}{pi }}=50Omega)
Tổng trở: (Z=sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}=sqrt{50^{2}+(100-50)^{2}}=50sqrt{2}Omega)
Bước 2: Định luật Ôm : Với Uo= IoZ = 5.50(sqrt{2}) = 250(sqrt{2})V;
Bước 3: Tính độ lệch pha giữa u hai đầu mạch và i: (tanvarphi =frac{Z_{L}-Z_{C}}{R}=frac{100-50}{50}=1Rightarrow varphi =frac{pi }{4})(rad).
Bước 4: Biểu thức điện áp tức thời giữa hai đầu mạch điện: (u=250sqrt{2}cos(100pi t+frac{pi }{4})(V))(V).
b.PHƯƠNG PHÁP DÙNG SỐ PHỨC TÌM BIỂU THỨC i HOẶC u
VỚI MÁY CASIO FX-570ES; FX-570ES PLUS;VINACAL-570ES PLUS .
(NHANH VÀ HIỆU QUẢ CHO TRẮC NGHIỆM)
1.Tìm hiểu các đại lượng xoay chiều dạng phức: Xem bảng liên hệ
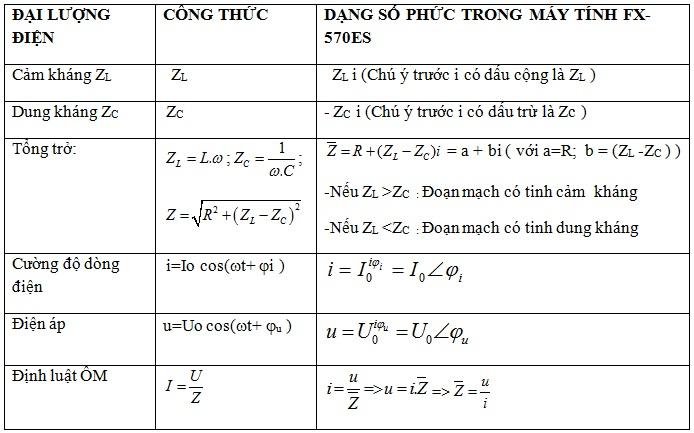
Chú ý: (bar{Z}=R+(Z_{L}-Z_{C})i)( tổng trở phức (bar{Z}) có gạch trên đầu: R là phần thực, (ZL -ZC ) là phần ảo)
Cần phân biệt chữ i sau giá trị b = (ZL -ZC ) là phần ảo , khác với chữ i là cường độ dòng điện
2.Chọn cài dặt máy tính: CASIO fx - 570ES ; 570ES Plus
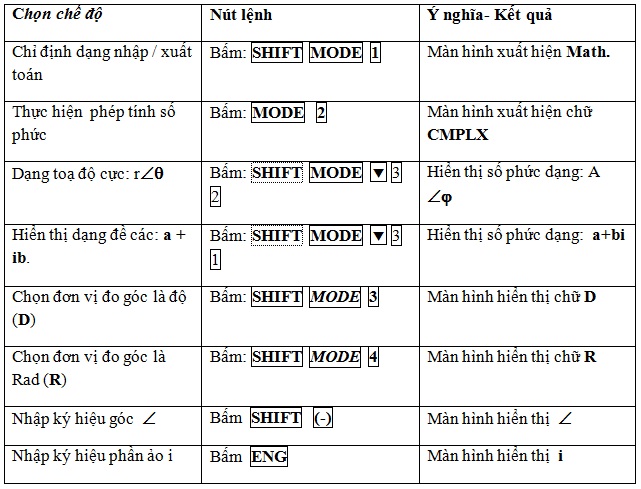
3.Lưu ý Chế độ hiển thị kết quả trên màn hình:
Sau khi nhập, ấn dấu = có thể hiển thị kết quả dưới dạng số vô tỉ,
muốn kết quả dưới dạng thập phân ta ấn SHIFT =
( hoặc nhấn phím S<=>D ) để chuyển đổi kết quả Hiển thị.
4. Các Ví dụ 1:
Ví dụ 1: Mạch điện xoay chiều gồm một điện trở thuần R = 50Ω, một cuộn thuần cảm có hệ số tự cảm (L=frac{1}{pi }(H)) và một tụ điện có điện dung (C=frac{2.10^{-4}}{pi }(F)) mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng (i=5cos100pi t(A)) .Viết biểu thức điện áp tức thời giữa hai đầu mạch điện.
Giải : (Z_{L}=omega L=100pi .frac{1}{pi }=100Omega ;Z_{C}=frac{1}{omega C}=...=50Omega) Và ZL-ZC =50Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : dạng hiển thị toạ độ cực:( r(angle)(Theta) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có :(u=i.bar{Z}=I_{0}angle varphi _{i}X(R+(Z_{L}-Z_{C}))i=5angle 0X(50+50i)) ( Phép NHÂN hai số phức)
Nhập máy: 5 SHIFT (-) 0 X ( 50 + 50 ENG i ) = Hiển thị: 353.55339(angle)45 = 250(sqrt{2})(angle)45
Vậy biểu thức tức thời điện áp của hai đầu mạch:
u = 250(sqrt{2}) cos( 100πt +π/4) (V).
Ví dụ 2: Một mạch điện xoay chiều RLC không phân nhánh có R = 100Ω; (C=frac{1}{pi }.10^{-4}F;L=frac{2}{pi }H). Cường độ dòng điện qua mạch có dạng: i = 2(sqrt{2})cos100πt(A). Viết biểu thức điện áp tức thời của hai đầu mạch?
Giải: . (Z_{L}=omega L=100pi .frac{2}{pi }=200Omega ;Z_{C}=frac{1}{omega C}=...=100Omega)Và ZL-ZC =100Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r(angle)(Theta) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có : (u=i.bar{Z}=I_{0}angle varphi _{i}X(R+(Z_{L}-Z_{C}))i=2sqrt{2}angle 0X(100+100i)) ( Phép NHÂN hai số phức)
Nhập máy: 2(sqrt{2}) (triangleright) SHIFT (-) 0 X ( 100 + 100 ENG i ) = Hiển thị: 400(angle)45
Vậy biểu thức tức thời điện áp của hai đầu mạch: u = 400cos( 100πt +π/4) (V).
Ví dụ 3: Cho đoạn mạch xoay chiều có R=40Ω, (L=frac{1}{pi }(H),C=frac{10^{-4}}{0,6pi }(F)), mắc nối tiếp điện áp 2 đầu mạch u=100(sqrt{2})cos100πt (V), Cường độ dòng điện qua mạch là:
A.(i=2,5cos(100pi t+frac{pi }{4})(A)) B.(i=2,5cos(100pi t-frac{pi }{4})(A))
C.(i=2cos(100pi t-frac{pi }{4})(A)) C.(i=2cos(100pi t+frac{pi }{4})(A))
Giải: (Z_{L}=omega L=100pi .frac{1}{pi }=100Omega ;Z_{C}=frac{1}{omega C}=frac{1}{100pi .frac{10^{-4}}{0,6pi }}=60Omega). Và ZL-ZC =40Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r(angle)(Theta) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có : (i=frac{u}{bar{Z}}=frac{U_{0}angle varphi _{u}}{(R+(Z_{L}-Z_{C}))i}=frac{100sqrt{2}angle 0}{(40+40i)}) ( Phép CHIA hai số phức)
Nhập 100(sqrt{2}) (triangleright) SHIFT (-) 0 : ( 40 + 40 ENG i ) = Hiển thị: 2,5(angle)-45
Vậy : Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 2,5cos(100πt -π/4) (A).
Chọn B
Ví dụ 4: Một đoạn mạch điện gồm điện trở R = 50Ω mắc nối tiếp với cuộn thuần cảm L = 0,5/π (H). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u = 100(sqrt{2})cos(100πt- π/4) (V). Biểu thức của cường độ dòng điện qua đoạn mạch là:
A. i = 2cos(100πt- π/2)(A). B. i = 2(sqrt{2})cos(100πt- π/4) (A).
C. i = 2(sqrt{2})cos100πt (A). D. i = 2cos100πt (A).
Giải: (Z_{L}=omega L=100pi .frac{0,5}{pi }=50Omega) Và ZL-ZC =50Ω - 0 = 50Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r(angle)(Theta) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có : (i=frac{u}{bar{Z}}=frac{U_{0}angle varphi _{u}}{(R+Z_{L}i}=frac{100sqrt{2}angle -45}{(50+50i)}) ( Phép CHIA hai số phức)
Nhập 100(sqrt{2}) (triangleright) SHIFT (-) - 45 : ( 50 + 50 ENG i ) = Hiển thị: 2(angle)- 90
Vậy : Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 2cos( 100πt - π/2) (A).
Chọn A
Ví dụ 5(ĐH 2009): Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm L = 1/4π (H) thì cường độ dòng điện 1 chiều là 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp u =150(sqrt{2})cos120πt (V) thì biểu thức cường độ dòng điện trong mạch là:
A.(i=5sqrt{2}cos(120pi t-frac{pi }{4})(A)) B. (i=5cos(120pi t+frac{pi }{4})(A))
C.(i=5sqrt{2}cos(120pi t+frac{pi }{4})(A)) D.(i=5cos(120pi t-frac{pi }{4})(A))
Giải: Khi đặt hiệu điện thế không đổi (hiệu điện thế 1 chiều) thì đoạn mạch chỉ còn có R: R = U/I =30Ω
(Z_{L}=omega L=120pi .frac{1}{4pi }=30Omega;i=frac{u}{bar{Z}}=frac{150sqrt{2}angle 0}{(30+30i)}) ( Phép CHIA hai số phức)
a.Với máy FX570ES :
-Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r(angle)(Theta) )
-Chọn đơn vị góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Nhập máy: 150(sqrt{2}) (triangleright) : ( 30 + 30 ENG i ) = Hiển thị: 5(angle)- 45
Vậy: Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 5cos( 120πt - π/4) (A).
Chọn D
b.Với máy FX570ES : -Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Chọn đơn vị góc là độ (R), bấm: SHIFT MODE 4 màn hình hiển thị R
Nhập máy: 150 (sqrt{2}) (triangleright) : ( 30 + 30 ENG i ) = Hiển thị dạng phức: 3.535533..-3.535533…i
Bấm SHIFT 2 3 : Hiển thị: 5(angle) - (frac{pi }{4})
Vậy: Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 5cos( 120πt - π/4) (A).
Chọn D


