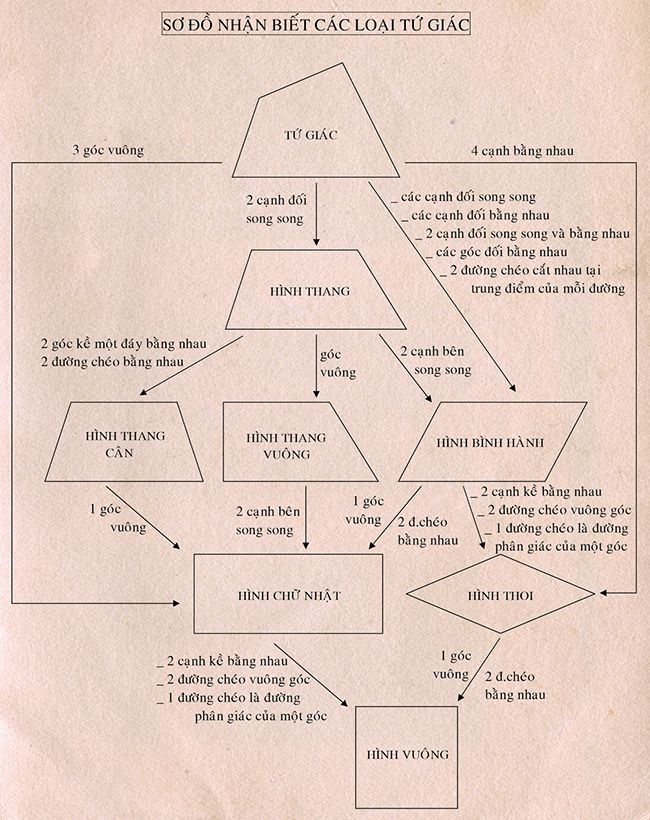
Để giải được dạng toán này, học sinh cần vận dụng linh hoạt các dấu hiệu nhận biết của các loại tứ giác đặc biệt (hình bình hành, hình thoi, hình chữ nhật, hình vuông)
1. Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là:
a. Hình chữ nhật; b. Hình thoi; c. Hình vuông.
Giải:
Trong ∆ ABC ta có EF là đường trung bình nên EF // AC và EF = 1/2AC (1)
Trong ∆ ADC ta có HG là đường trung bình nên HG // AC và HG = 1/2AC (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành
a. Tứ giác EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AC ⊥ BD
b. Tứ giác EFGH là hình thoi ⇔ EH = EF ⇔ AC = BD
c. Tứ giác EFGH là hình vuông ⇔ AC ⊥ BD và AC = BD
2. Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
a. Tứ giác AEDF là hình gì ? Vì sao ?
b. Các tứ giác ADBM, ADCN là hình gì ? Vì sao ?
c. Chứng minh rằng M đối xứng với N qua A
d. Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông ?
Giải:
a. Điểm M và điểm D đối xứng qua trục AB
⇒ AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM
⇒ AED=900
Điểm D và điểm N đối xứng nhau qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN
⇒ AC ⊥ DN ⇒ˆAFD=900
ˆEAF=900
Vậy tứ giác AEDF là hình chữ nhật (vì có ba góc vuông)
b. Tứ giác AEDF là hình chữ nhật ⇒ DE // AC; DF // AB
Trong ∆ ABC ta có: DB = DC (gt)
DE // AC
Suy ra: AE = EB (tính chất đường trung bình tam giác);
DF// AB
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM : AE = EB (chứng minh trên)
ED = EM (vì AB là trung trực DM)
Suy ra: Tứ giác ADBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi ( vì có hai đường chéo vuông góc)
Xét tứ giác ADCN:
AF = FC (chứng minh trên)
DF = FN (vì AC là đường trung trực DN)
Suy ra: Tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo vuông góc)
c. Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trung với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng với nhau qua điểm A
d. Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = 1/2AB ; AF =1/2AC
nên AE = AF suy ra AB = AC
Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.
2. Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, CD, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:
a. Hình chữ nhật; b. Hình thoi; c. Hình vuông.
Giải:
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có: HB = HD, GD = GC (gt)
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
a) EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC
b) EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC
c) EFGH là hình vuông ⇔ AD ⊥ BC và AD = BC
3. Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC.
a. Chứng minh rằng tứ giác DEHK là hình bình hành.
b. Tam giác ABC có điều kiện gì thì tứ giác DEHK là hình chữ nhật ?
c. Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì ?
Giải:
a. Ta có: GD = 1/2GB (tính chất đường trung tuyến của tam giác)
GH = 1/2GB (gt)
Suy ra: GD = GH
GE = 1/2GC (tính chất đường trung tuyến của tam giác)
GK = 1/2GC (gt)
Suy ra: GE = GK
Tứ giác DEHK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
b. Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK
mà DH = 1/2BD; EK = 1/2CE
nên DH = EK ⇒ BD = CE ⇒ ∆ ABC cân tại A
Vậy ∆ ABC cân tại A thì tứ giác DEHK là hình chữ nhật.
c. Nếu BD ⊥ CE ⇒ DH ⊥ EK
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.
4. Cho hình bình hành ABCD có AB = 2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD.
a. Các tứ giác AEFD, AECF là hình gì ? Vì sao ?
b. Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
c. Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông ?
Giải:
a. Xét tứ giác AEFD:
AB // CD (gt) hay AE // FD
AE = 1/2AB (gt); FD = 1/2CD (gt)
Suy ra: AE = FD
Tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
AD = AE = 1/2AB
Vậy tứ giác AEFD là hình thoi.
Xét tứ giác AECF : AE // CF (gt), AE = 1/2AB (gt), CF = 1/2CD (gt)
Suy ra: AE = CF
Tứ giác AECF là hình bình hành (vì có một cặp canh đối song song và bằng nhau)
b. Tứ giác AECF là hình thoi ⇒ AF ⊥ ED ⇒ ˆEMF=900
AF // CE (vì tứ giác AECF là hình bình hành)
Suy ra: CE ⊥ ED ⇒ˆMEN=900
Xét tứ giác EBFD ta có: EB = FD (vì cùng bằng AE)
EB // FD (vì AB // CD)
Xét tứ giác EBFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ DE // BF
Suy ra: BF ⊥ AF ⇒ góc MFE = 1v
Vậy tứ giác EMFN là hình chữ nhật.
c. Ta có: Hình chữ nhật EMFN là hình vuông ⇔ ME = MF
⇔ DE = AF (vì ME = 1/2DE , MF = 1/2AF - tính chất hình thoi)
⇔ AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇔ A=900 ⇔ Hình bình hành ABCD là hình chữ nhật
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB =2AD.
5. Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC.
a. Chứng minh rằng ADEF là hình thoi
b. Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông ?
Giải:
a. Ta có: E là trung điểm của BC (gt), D là trung điểm của AB (gt)
nên ED là đường trung bình của ∆ ABC
DE = AF = 1/2AC (1)
F là trung điểm của AC (gt) nên EF là đường trung bình ∆ ABC ⇒ EF = AD = 1/2AB (2)
AB = AC (gt)
Từ (1), (2) và (gt) suy ra: AD = DE = EF = AF
Vậy tứ giác ADEF là hình thoi.
b. Hình thoi ADEF là hình vuông ⇒ ˆA=900
⇒ ∆ ABC vuông cân tại A
Ngược lại nếu ∆ ABC vuông cân tại A
⇒ Tứ giác ADEF là hình thoi có ˆA=900
⇒ Hình thoi ADEF là hình vuông
Vậy hình thoi ADEF là hình vuông thì ∆ ABC vuông cân tại A.


